Logaritma

Grafik fungsi logaritma dengan tiga bilangan pokok yang umum. Titik khusus Templat:Math diperlihatkan oleh garis bertitik, dan semua kurva fungsi memotong di Templat:Math.

Dalam matematika, logaritma adalah fungsi invers dari eksponensiasi. Dengan kata lain, logaritma dari Templat:Mvar adalah eksponen dengan bilangan pokok Templat:Mvar yang dipangkatkan dengan bilangan konstan lain agar memperoleh nilai Templat:Mvar. Kasus sederhana dalam logaritma adalah menghitung jumlah munculnya faktor yang sama dalam perkalian berulang. Sebagai contoh, Templat:Math dibaca, "logaritma 1000 dengan bilangan pokok 10 sama dengan 3" atau dinotasikan sebagai Templat:Math. Logaritma dari Templat:Mvar dengan bilangan pokok Templat:Mvar dilambangkan Templat:Math. Terkadang logaritma dilambangkan sebagai Templat:Math atau tanpa menggunakan tanda kurung, Templat:Math, atau bahkan tanpa menggunakan bilangan pokok khusus, Templat:Math.

Ada tiga bilangan pokok logaritma yang umum beserta kegunaannya. Logaritma dengan bilangan pokok Templat:Math (Templat:Math) disebut sebagai logaritma umum, yang biasanya dipakai dalam ilmu sains dan rekayasa. Logaritma dengan dengan bilangan pokok [[E (konstanta matematika)|bilangan Templat:Math]] (Templat:Math) disebut sebagai logaritma alami, yang dipakai dengan luas dalam matematika dan fisika, karena dapat mempermudah perhitungan integral dan turunan. Logaritma dengan bilangan pokok Templat:Math (Templat:Math) disebut sebagai logaritma biner, yang seringkali dipakai dalam ilmu komputer.

Logaritma diperkenalkan oleh John Napier pada tahun 1614 sebagai alat yang menyederhanakan perhitungan. Logaritma dipakai lebih cepat dalam navigator, ilmu sains, rekayasa, ilmu ukur wilayah, dan bidang lainnya untuk lebih mempermudah perhitungan nilai yang sangat akurat. Dengan menggunakan tabel logaritma, cara yang membosankan seperti mengalikan digit yang banyak dapat digantikan dengan melihat tabel dan penjumlahan yang lebih mudah. Ini dapat dilakukan karena logaritma dari hasil kali bilangan merupakan logaritma dari jumlah faktor bilangan:

$b^{}\log (xy)={}^b\log x+{}^b\log y,$

asalkan bahwa Templat:Mvar, Templat:Mvar dan Templat:Mvar bilangan positif dan Templat:Math. Mistar hitung yang juga berasal dari logaritma dapat mempermudah perhitungan tanpa menggunakan tabel, namun perhitungannya kurang akurat. Leonhard Euler mengaitkan gagasan logaritma saat ini dengan fungsi eksponensial pada abad ke-18, dan juga memperkenalkan huruf Templat:Mvar sebagai bilangan pokok dari logaritma alami.

Penerapan skala logaritmik dipakai dalam mengurangi kuantitas yang sangat besar menjadi lebih kecil. Sebagai contoh, desibel (dB) adalah satuan yang digunakan untuk menyatakan rasio sebagai logaritma, sebagian besar untuk kekuatan sinyal dan amplitudo (contoh umumnya pada tekanan suara). Dalam kimia, pH mengukur keasaman dari larutan berair melalui logaritma. Logaritma umumnya dipakai dalam rumus ilmiah, dalam pengukuran kompleksitas algoritma dan objek geometris yang disebut sebagai fraktal. Logaritma juga membantu untuk menjelaskan frekuensi rasio interval musik, ditemukan di rumus yang menghitung bilangan prima atau hampiran faktorial, memberikan gambaran dalam psikofisika, dan dapat membantu perhitungan akuntansi forensik.

Konsep logaritma sebagai invers dari eksponensiasi juga memperluas ke struktur matematika lain. Namun pada umumnya, logaritma cenderung merupakan fungsi bernilai banyak. Sebagai contoh, logaritma kompleks merupakan invers dari fungsi eksponensial pada bilangan kompleks. Mirip dengan contoh sebelumnya, logaritma diskret dalam grup hingga, merupakan invers fungsi eksponensial bernilai banyak yang memiliki kegunaan dalam kriptografi kunci publik.

Alasan

Gambar memperlihatkan grafik logaritma dengan bilangan pokok 2 memotong sumbu-x di Templat:Math dan melalui titik Templat:Nowrap, Templat:Nowrap, dan Templat:Nowrap, sebagai contoh, Templat:Math dan Templat:Math. Grafik tersebut dengan sembarang mendekati sumbu-Templat:Mvar, namun tidak mendekati sumbu-x.

Operasi aritmetika yang paling dasar adalah penambahan, perkalian, dan eksponen. Kebalikan dari penambahan adalah pengurangan, dan kebalikan dari perkalian adalah pembagian. Mirip dengan contoh sebelumnya, logaritma merupakan kebalikan (atau invers) dari operasi eksponensiasi. Eksponensiasi adalah bilangan bilangan pokok Templat:Mvar yang ketika dipangkatkan dengan Templat:Mvar memberikan nilai Templat:Mvar. Ini dirumuskan sebagai

$b^y=x.$

Sebagai contoh, Templat:Math pangkat Templat:Math memberikan nilai Templat:Math. Secara matematis, $2^3=8$.

Logaritma dengan bilangan pokok Templat:Mvar adalah operasi invers yang menyediakan nilai keluaran Templat:Mvar dari nilai masukan Templat:Mvar. Hal ini mengartikan bahwa Templat:Math ekuivalen dengan Templat:Math, jika Templat:Mvar bilangan real positif. (Jika Templat:Mvar bukanlah bilangan real positif, eksponensiasi dan logaritma dapat terdefinisi tetapi membutuhkan beberapa nilai, sehingga definisi darinya semakin rumit.)

Salah satu alasan bersejarah utamanya dalam memperkenalkan logaritma adalah rumus

$b^{}\log (xy)={}^b\log x+{}^b\log y,$

yang dapat mempermudah perhitungan nilai perkalian dan pembagian dengan penjumlahan, pengurangan, dan melihat tabel logaritma. Perhitungan ini dipakai sebelum komputer ditemukan.

Definisi

Diberikan bilangan real positif Templat:Mvar sehingga Templat:Math, maka logaritma dari bilangan real positif Templat:Mvar terhadap bilangan pokok Templat:MvarTemplat:Refn adalah eksponen dengan bilangan pokok Templat:Mvar yang dipangkatkan bilangan agar memperoleh nilai Templat:Mvar. Dengan kata lain, logaritma bilangan pokok Templat:Mvar dari Templat:Mvar adalah bilangan real Templat:Mvar sehingga Templat:Math. Logaritma dilambangkan sebagai Templat:Math (dibaca "logaritma Templat:Mvar dengan bilangan pokok Templat:Mvar"). Terdapat definisi yang mirip dan lebih ringkas mengatakan bahwa fungsi Templat:Math invers dengan fungsi Templat:Math.

Sebagai contoh, Templat:Math, karena Templat:Math. Logaritma juga dapat bernilai negatif, contohnya Templat:Math, karena Templat:Math. Logaritma juga berupa nilai desimal, sebagai contoh Templat:Math kira-kira sama dengan 2,176 karena terletak di antara 2 dan 3, dan begitupula 150 terletak antara Templat:Math dan Templat:Math. Adapun sifat logaritma bahwa untuk setiap Templat:Mvar, Templat:Math karena Templat:Math, dan Templat:Math karena Templat:Math.

Identitas logaritma

Templat:Main Ada beberapa rumus penting yang mengaitkan logaritma dengan yang lainnya.

Hasil kali, hasil bagi, pangkat, dan akar

Logaritma dari hasil kali merupakan jumlah logaritma dari bilangan yang dikalikan, dan logaritma dari hasil bagi dari dua bilangan merupakan selisih logaritma. Logaritma dari bilangan pangkat ke-Templat:Mvar sama dengan Templat:Mvar dikali logaritma dari bilangan tersendiri, dan logaritma bilangan akar ke-Templat:Mvar sama dengan logaritma dibagi dengan Templat:Mvar. Tabel berikut memuat daftar sifat-sifat logaritma tersebut beserta contohnya. Masing-masing identitas ini diperoleh dari hasil substitusi dari definisi logaritma $x=b^{{}^b\log x}$ atau $y=b^{{}^b\log y}$ pada ruas kiri persamaan.

	Rumus	Contoh
Hasil kali	$b^{}\log (xy)={}^b\log x+{}^b\log y$	$3^{}\log 243={}^3\log (9\cdot 27){=}^3\log 9+{}^3\log 27=2+3=5$
Hasil bagi	$b^{}\log \frac{x}{y}={}^b\log x-{}^b\log y$	$2^{}\log 16={}^2\log \frac{64}{4}={}^2\log 64-{}^2\log 4=6-2=4$
Pangkat	$b^{}\log \left(x^p\right)=p{}^b\log x$	$2^{}\log 64={}^2\log \left(2^6\right)=6\cdot {}^2\log 2=6$
Akar	$b^{}\log \sqrt[p]{x}=\frac{{}^b\log x}{p}$	${10}^{}\log \sqrt{1000}=\frac{1}{2}\cdot {}^{10}\log 1000=\frac{3}{2}=1,5$

Mengubah bilangan pokok

Logaritma Templat:Math dapat dihitung sebagai hasil bagi logaritma Templat:Mvar dengan logaritma Templat:Mvar terhadap bilangan pokok sembarang Templat:Mvar. Secara matematis dirumuskan sebagai:

$b^{}\log x=\frac{{}^k\log x}{{}^k\log b}.$

Templat:Collapse top Dimulai dari identitas berikut

$x=b^{{}^b\log x},$

ini dapat menerapkan Templat:Math pada kedua ruas sehingga memperoleh

$k^{}\log x={}^k\log \left(b^{{}^b\log x}\right)={}^b\log x\cdot {}^k\log b$.

Ketika mencari penyelesaian untuk Templat:Math, maka menghasilkan persamaan:

$b^{}\log x=\frac{{}^k\log x}{{}^k\log b}$.

Hal ini memperlihatkan faktor konversi dari nilai Templat:Math ke nilai Templat:Math yang serupa agar memperoleh bentuk Templat:Math Templat:Collapse bottomKalkulator ilmiah merupakan alat yang menghitung logaritma dengan bilangan pokok 10 dan Templat:Mvar. Logaritma terhadap setiap bilangan pokok Templat:Mvar dapat ditentukan menggunakan kedua logaritma tersebut melalui rumus sebelumnya:

$b^{}\log x=\frac{{}^{10}\log x}{{}^{10}\log b}=\frac{{}^e\log x}{{}^e\log b}.$

Diberikan suatu bilangan Templat:Mvar dan logaritma Templat:Math, dengan Templat:Mvar adalah bilangan pokok yang tidak diketahui. Bilangan pokok tersebut dapat dinyatakan dengan

$b=x^{\frac{1}{y}},$

Rumus ini dapat diperlihatkan dengan mengambil persamaan yang mendefinisikan Templat:Math, lalu dipangkatkan dengan Templat:Math.

Bilangan pokok khusus

Grafik logaritma dengan bilangan pokok 0,5; 2; dan Templat:Mvar

Secara khusus, terdapat tiga bilangan pokok yang umum di antara semua pilihan bilangan pokok pada logaritma. Ketiga bilangan pokok tersebut adalah Templat:Math, Templat:Math (konstanta bilangan irasional yang kira-kira sama dengan 2,71828), dan Templat:Math (logaritma biner). Dalam analisis matematika, logaritma dengan bilangan pokok Templat:Mvar tersebar karena sifat analitik yang dijelaskan di bawah. Di sisi lain, logaritma dengan Templat:Nowrap mudah dipakai dalam perhitungan manual dalam sistem bilangan desimal:

${10}^{}\log (10x)={}^{10}\log 10+{}^{10}\log x=1+{}^{10}\log x.$

Jadi, Templat:Math berkaitan dengan jumlah digit desimal dari bilangan bulat positif Templat:Mvar: jumlah digitnya merupakan bilangan bulat terkecil yang lebih besar dari Templat:Math. Sebagai contoh, Templat:Math kira-kira sama dengan 3,15. Bilangan berikutnya merupakan jumlah digit dari 1430, yaitu 4. Dalam teori informasi, logaritma alami dipakai dalam nat dan logaritma dengan bilangan pokok 2 dipakai dalam bit sebagai satuan dasar informasi. Logaritma biner juga dipakai dalam ilmu komputer, dengan sistem biner ditemukan dimana-mana. Dalam teori musik, rasio tinggi nada kedua (yaitu oktaf) ditemukan dimana-mana dan jumlah sen antara setiap dua tinggi nada dirumuskan sebagai konstanta 1200 dikali logaritma dari rasio (yaitu, 100 sen per setengah nada dengan temperamen sama). Dalam fotografi, logaritma dengan bilangan pokok dua dipakai untuk mengukur nilai pajanan, tingkatan cahaya, waktu eksposur, tingkap, dan kecepatan film dalam "stop".

Tabel berikut memuat notasi-notasi umum mengenai bilangan pokok beserta bidang yang dipakai. Selain Templat:Math, adapula notasi logaritma lain yang ditulis sebagai Templat:Math, dan juga seperti Templat:Math. Pada kolom "Notasi ISO" memuat penamaan yang disarankan Organisasi Standardisasi Internasional, yakni ISO 80000-2. Karena notasi Templat:Math telah dipakai untuk ketiga bilangan pokok di atas (atau ketika bilangan pokok belum ditentukan), bilangan pokok yang dimaksud harus sering diduga tergantung konteks atau bidangnya. Sebagai contoh, Templat:Math biasanya mengacu pada Templat:Math dalam ilmu komputer, dan Templat:Math mengacu pada Templat:Math. Dalam konteks lainnya, Templat:Math seringkali mengacu pada Templat:Math.

Bilangan pokok	Nama Templat:Math	Notasi ISO	Notasi lain	Dipakai dalam bidang
2	logaritma biner	Templat:Math	Templat:Math, Templat:Math, Templat:Math, Templat:Math	ilmu komputer, teori informasi, bioinformatika, teori musik, fotografi
Templat:Mvar	logaritma alami	Templat:MathTemplat:Refn	Templat:Math (dipakai dalam matematika dan beberapa bahasa pemrograman lainnyaTemplat:Refn), Templat:Math	matematika, fisika, kimia, statistik, ekonomi, teori informasi, dan rekayasa
10	logaritma biasa	Templat:Math	Templat:Math, Templat:Math (dipakai dalam rekayasa, biologi, dan astronomi)	bidang berbagai rekayasa (lihat desibel dan lihat di bawah), tabel logaritma, kalkulator genggam, spektroskopi
Templat:Mvar	logaritma dengan bilangan pokok Templat:Mvar	Templat:Math		matematika

Sejarah

Templat:Main Sejarah logaritma yang dimulai dari Eropa pada abad ketujuh belas merupakan penemuan fungsi terbaru yang memperluas dunia analisis di luar keterbatasan metode aljabar. Metode logaritma dikemukakan secara terbuka oleh John Napier pada tahun 1614, dalam bukunya yang berjudul Mirifici Logarithmorum Canonis Descriptio. Namun, teknik-teknik lain sebelum penemuan Napier sudah ada dengan keterbatasan metode yang serupa, contohnya seperti prosthafaeresis atau penggunaan tabel barisan, yang dikembangkan dengan luas oleh Jost Bürgi sekitar tahun 1600. Napier menciptakan istilah untuk logaritma dalam bahasa Latin Tengah, “logaritmus”, yang berasal dari gabungan dua kata Yunani, logos “proporsi, rasio, kata” + arithmos “bilangan”. Secara harfiah, "logaritmus" berarti “bilangan rasio”.

Logaritma umum dari bilangan adalah indeks dari perpangkatan sepuluh yang sama dengan bilangan tersebut. Bilangan yang sangat membutuhkan banyak angka merupakan kiasan kasar untuk logaritma umum, dan Archimedes menyebutnya sebagai “orde bilangan”. Logaritma real pertama adalah metode heuristik yang mengubah perkalian menjadi penjumlahan, sehingga memudahkan perhitungan yang cepat. Ada beberapa metode yang menggunakan tabel yang diperoleh dari identitas trigonometri, dan metode tersebut dinamakan prosthafaeresis.

Penemuan fungsi yang dikenal saat ini sebagai logaritma alami, berawal dari saat Grégoire de Saint-Vincent mencoba menggambarkan kuadratur hiperbola persegi panjang. Archimedes menulis risalah yang berjudul The Quadrature of the Parabola pada abad ke-3 SM, tetapi kuadratur hiperbola menghindari semua upayanya hingga Saint-Vincent menerbitkan hasilnya pada tahun 1647. Logaritma yang mengaitkan barisan dan deret geometri dalam argumen dan nilai barisan dan deret aritmetika, meminta Antonio de Sarasa untuk mengaitkan kuadratur Saint-Vincent dan tradisi logaritma dalam prosthafaeresis sehingga mengarah ke sebuah persamaan kata untuk logaritma alami, yaitu "logaritma hiperbolik". Christiaan Huygens dan James Gregory mulai mengenali fungsi baru tersebut. Leibniz memakai notasi Log y pada tahun 1675, dan tahun berikutnya ia mengaitkannya dengan integral

$\int \frac{dy}{y}.$

Sebelum Euler mengembangkan konsep modernnya tentang logaritma alami kompleks, Roger Cotes memperlihatkan hasil yang hampir sama pada tahun 1714 bahwa

$\log (\cos \theta +i\sin \theta )=i\theta$.

Tabel logaritma, mistar hitung, dan penerapan bersejarah

Penjelasan logaritma dalam Encyclopædia Britannica pada tahun 1797.

Dengan menyederhanakan perhitungan yang rumit sebelum adanya mesin hitung komputer, logaritma berkontribusi pada kemajuan pengetahuan, khususnya astronomi. Logaritma sangat penting terhadap kemajuan dalam survei, navigasi benda langit, dan cabang lainnya. Pierre-Simon Laplace menyebut logaritma sebagai

"...kecerdasan yang mengagumkan, [sebuah alat] yang mengurangi pekerjaan berbulan-bulan menjadi beberapa hari, menggandakan kehidupan astronom, dan menghindarinya dari kesalahan dan rasa jijik yang tak terpisahkan dari perhitungan yang panjang."

Templat:AnchorKarena fungsi Templat:Math adalah fungsi invers dari Templat:Math, maka fungsi tersebut disebut sebagai antilogaritma. Saat ini, antilogaritma lebih sering disebut fungsi eksponensial.

Tabel logaritma

Sebuah alat penting yang memungkinkan penggunaan logaritma adalah tabel logaritma. Tabel logaritma pertama kali disusun oleh Henry Briggs pada tahun 1617 setelah penemuan Napier, tetapi penemuannya menggunakan 10 sebagai bilangan pokok. Tabel pertamanya memuat logaritma umum dari semua bilangan bulat yang berkisar antara 1 dengan 1000, dengan ketepatan yang dimiliki 14 digit, dan kemudian ia membuat tabel dengan kisaran yang besar. Tabel tersebut mencantumkan nilai ${10}^{}\log x$ untuk setiap bilangan $x$ dalam kisaran dan ketepatan tertentu. Karena bilangan yang berbeda dengan faktor 10 memiliki logaritma yang berbeda dengan bilangan bulat, logaritma dengan bilangan pokok 10 digunakan secara universal untuk perhitungan, sehingga disebut logaritma umum. Logaritma umum dari $x$ dipisahkan menjadi bagian bilangan bulat yang dikenal sebagai karakteristik, dan bagian pecahan (Templat:Lang-en) yang dikenal sebagai mantissa. Tabel logaritma hanya perlu menyertakan mantissa, karena karakteristik logaritma umum dapat dengan mudah ditentukan dengan menghitung angka dari titik desimal. Karakteristik logaritma umum dari $10\cdot x$ sama dengan satu ditambah karakteristik $x$, dan mantissanya sama. Dengan menggunakan tabel logartima dengan tiga digit, nilai logaritma dari 3542 kira-kira sama dengan

${10}^{}\log 3542={}^{10}\log (1000\cdot 3,542)=3+{}^{10}\log 3,542\approx 3+{}^{10}\log 3,54$

Nilainya dengan ketepatan yang sangat tinggi dapat diperoleh melalui interpolasi:

${10}^{}\log 3542\approx 3{+}^{10}\log 3,54+0,2\cdot ({}^{10}\log 3,55-{}^{10}\log 3,54)$

Nilai $10^x$ dapat ditentukan dengan pencarian terbalik pada tabel yang sama, karena logaritma merupakan fungsi monoton.

Perhitungan

Hasil kali atau hasil bagi dari dua bilangan positif Templat:Mvar dan Templat:Mvar biasanya dihitung sebagai penambahan dan pengurangan logaritma. Hasil kali Templat:Math berasal dari antilogaritma dari penambahan dan hasil bagi Templat:Math berasal dari antilogaritma dari pengurangan, melalui tabel yang sama:

$cd=10^{{}^{10}\log c}10^{{}^{10}\log d}=10^{{}^{10}\log c+{}^{10}\log d}$

dan

$\frac{c}{d}=c{d}^{-1}=10^{{}^{10}\log c-{}^{10}\log d}.$

Untuk perhitungan manual yang meminta ketelitian yang cukup besar, melakukan pencarian kedua logaritma, menghitung jumlah atau selisihnya, dan mencari antilogaritma jauh lebih cepat daripada menghitung perkalian dengan metode sebelumnya seperti prosthafaeresis, yang mengandalkan identitas trigonometri.

Perhitungan pangkat direduksi menjadi perkalian, dan sedangkan perhitungan akar direduksi menjadi pembagian. Pernyataan ini dapat dilihat sebagai

$c^d={\left(10^{{}^{10}\log c}\right)}^d=10^{d{}^{10}\log c}$

dan

$\sqrt[d]{c}=c^{\frac{1}{d}}=10^{\frac{1}{d}{}^{10}\log c}.$

Perhitungan trigonometri dilengkapi dengan tabel-tabel yang memuat logaritma umum dari fungsi trigonometri.

Mistar hitung

Penerapan penting lainnya adalah mistar hitung, sepasang skala yang dibagi secara logaritmik yang digunakan dalam perhitungan. Adapun skala logaritmik yang tidak memiliki sorong, mistar Gunter, ditemukan tak lama setelah penemuan Napier dan disempurnakan oleh William Oughtred untuk menciptakan sepasang skala logaritmik yang dapat dipindahkan terhadap satu sama lain, yaitu mistar hitung. Angka yang ditempatkan pada skala hitung pada jarak sebanding dengan selisih antara logaritmanya. Menggeser skala atas dengan tepat berarti menambahkan logaritma secara mekanis, seperti yang diilustrasikan berikut ini:

Penggambaran skema mengenai mistar hitung. Dimulai dari 2 pada skala di bawah, lalu tambahkan dengan jarak ke 3 pada skala atas agar mencapai hasil kali 6. Mistar hitung bekerja karena ditandai sedemikian rupa sehingga jarak dari 1 ke Templat:Math sebanding dengan logaritma Templat:Math.

Sebagai contoh, dengan menambahkan jarak dari 1 ke 2 pada skala di bagian bawah ke jarak dari 1 ke 3 pada skala di bagian atas menghasilkan hasil kali 6, yang dibacakan di bagian bawah. Mistar hitung adalah sebuah alat menghitung yang penting bagi para insinyur dan ilmuwan hingga tahun 1970-an, karena dengan mengorbankan ketepatan nilai memungkinkan perhitungan yang jauh lebih cepat daripada teknik berdasarkan tabel.

Sifat analitik

Kajian yang lebih dalam mengenai logaritma memerlukan sebuah konsep yang disebut fungsi. Fungsi merupakan sebuah kaidah yang dipetakan suatu bilangan akan menghasilkan bilangan lain. Contohnya seperti fungsi yang menghasilkan bilangan konstan Templat:Mvar, yang dipangkatkan setiap bilangan real Templat:Mvar. Fungsi ini secara matematis ditulis sebagai Templat:Math. Ketika Templat:Mvar positif dan tak sama dengan 1, maka Templat:Mvar adalah fungsi terbalikkan ketika dianggap sebagai fungsi dengan interval dari bilangan real ke bilangan real positif.

Keberadaan

Misalkan Templat:Mvar adalah bilangan real positif yang tidak sama dengan 1 dan misalkan Templat:Math. Pernyataan yang diikuti dari teorema nilai antara ini, merupakan hasil standar dalam analisis real yang mengatakan bahwa setiap fungsi monoton sempurna dan kontinu merupakan fungsi bijektif antara ranah (Templat:Lang-en) dan kisarannya (Templat:Lang-en). Pernyataan saat ini mengatakan bahwa Templat:Mvar yang menaik sempurna (untuk Templat:Math), atau menurun sempurna (untuk Templat:Math) merupakan fungsi kontinu, memiliki ranah $ℝ$ dan memiliki kisaran ${ℝ}_{>0}$. Oleh karena itu, Templat:Mvar adalah fungsi bijeksi dari $ℝ$ ke ${ℝ}_{>0}$. Dengan kata lain, untuk setiap bilangan real positif Templat:Mvar, terdapat setidaknya satu bilangan real Templat:Mvar sehingga $b^x=y$.

Misalkan $b^{}\log :{ℝ}_{>0}\to ℝ$ yang menyatakan invers dari fungsi Templat:Mvar. Dalam artian, Templat:Math adalah bilangan real tunggal Templat:Mvar sehingga $b^x=y$. Fungsi ini disebut fungsi logaritma dengan bilangan pokok-Templat:Mvar atau fungsi logaritmik (atau logaritma saja).

Karakterisasi melalui rumus hasil kali

Pada dasarnya, fungsi Templat:Math juga dapat dikarakterisasikan melalui rumus hasil kali

$b^{}\log (xy)={}^b\log x+{}^b\log y.$

Lebih tepatnya, logaritma untuk setiap bilangan pokok Templat:Math yang hanya merupakan [[Fungsi menaik|fungsi Templat:Math naik]] dari bilangan real positif ke bilangan real memenuhi sifat bahwa Templat:Math dan

$f(xy)=f(x)+f(y).$

Grafik fungsi logaritma

Grafik fungsi logaritma Templat:Math (berwarna biru) diperoleh dengan mencerminkan grafik fungsi Templat:Math (berwarna merah) di garis diagonal(Templat:Math).

Seperti yang dibahas sebelumnya, fungsi Templat:Math invers terhadap fungsi eksponensial $x\mapsto b^x$. Karena itu, grafiknya berkorespondensi dengan satu sama lain saat menukar koordinat-Templat:Mvar dan koordinat-Templat:Mvar (atau saat melakukan pencerminan di garis diagonal Templat:Math), seperti yang diperlihatkan sebagai berikut: sebuah titik Templat:Math pada grafik dari Templat:Mvar menghasilkan sebuah titik Templat:Math pada grafik logaritma dan sebaliknya. Akibatnya, Templat:Math divergen menuju takhingga (dalam artian semakin besar dari setiap bilangan yang diberikan) jika Templat:Mvar naik menuju takhingga, asalkan Templat:Mvar lebih besar dari satu. Pada kasus tersebut, Templat:Math merupakan fungsi menaik. Sedangkan untuk kasus Templat:Math, Templat:Math cenderung menuju ke negatif takhingga. Ketika Templat:Mvar mendekati nol, Templat:Math menuju ke negatif takhingga untuk Templat:Math dan menuju ke plus takhingga untuk Templat:Math.

Turunan dan antiturunan

Grafik fungsi logaritma alami (berwarna hijau) beserta garis singgungnya di Templat:Math (berwarna hitam)

Sifat analitik tentang fungsi adalah melalui fungsi inversnya. Jadi, ketika Templat:Math adalah fungsi kontinu dan terdiferensialkan, maka Templat:Math fungsi kontinu dan terdiferensialkan juga. Penjelasan kasarnya, sebuah fungsi kontinu adalah terdiferensialkan jika grafiknya tidak mempunyai "ujung" yang tajam. Lebih lanjut, ketika turunan dari Templat:Math menghitung nilai Templat:Math melalui sifat-sifat fungsi eksponensial, aturan rantai menyiratkan bahwa turunan dari Templat:Math dirumuskan sebagai

$\frac{d}{dx}{}^b\log x=\frac{1}{x\ln b}.$

Artinya, kemiringan dari garis singgung yang menyinggung grafik logaritma dengan bilangan pokok Templat:Math di titik Templat:Math sama dengan Templat:Math.

Turunan dari Templat:Math adalah Templat:Math, yang berarti ini menyiratkan bahwa Templat:Math adalah integral tunggal dari Templat:Math yang mempunyai nilai 0 untuk Templat:Math. Hal ini merupakan rumus paling sederhana yang mendorong sifat "alami" pada logaritma alami, dan hal ini juga merupakan salah satu alasan pentingnya konstanta [[E (konstanta matematika)|Templat:Mvar]].

Turunan dengan argumen fungsional rampat Templat:Math dirumuskan sebagai

$\frac{d}{dx}\ln f(x)=\frac{f^{\prime }(x)}{f(x)}.$

Hasil bagi pada ruas kanan disebut turunan logaritmik dari Templat:Mvar dan menghitung Templat:Math melalui turunan dari Templat:Math dikenal sebagai pendiferensialan logaritmik. Antiturunan dari logaritma alami Templat:Math dirumuskan sebagai:

$\int \ln (x)dx=x\ln (x)-x+C.$

Terdapat rumus yang berkaitan, seperti antiturunan dari logaritma dengan bilangan pokok lainnya dapat diperoleh dari persamaan ini dengan mengubah bilangan pokoknya.

Representasi integral mengenai fungsi logaritma

Logaritma natural dari Templat:Mvar adalah luas yang diwarnai di bawah grafik fungsi Templat:Math.

Logaritma alami dari Templat:Mvar dapat didefinisikan sebagai integral tentu:

$\ln t=\underset{1}{\overset{t}{\int }}\frac{1}{x}dx.$

Definisi ini menguntungkan karena tidak bergantung pada fungsi eksponensial atau fungsi trigonometri apapun, dan definisi ini merupakan sebuah integral dari fungsi timbal balik sederhana. Penjelasan dalam integral, Templat:Math sama dengan luas antara sumbu-Templat:Mvar dan grafik fungsi Templat:Math, yang berkisar dari Templat:Math ke Templat:Math. Penjelasan ini juga merupakan akibat dari teorema dasar kalkulus, dan bahkan turunan dari Templat:Math sama dengan Templat:Math. Rumus logaritma hasil kali dan pangkat dapat diperoleh melalui definisi ini. Sebagai contoh, rumus hasil kali Templat:Math dapat disimpulkan sebagai:

$\ln (tu)=\underset{1}{\overset{tu}{\int }}\frac{1}{x}dx\stackrel{(1)}{=}\underset{1}{\overset{t}{\int }}\frac{1}{x}dx+\underset{t}{\overset{tu}{\int }}\frac{1}{x}dx\stackrel{(2)}{=}\ln (t)+\underset{1}{\overset{u}{\int }}\frac{1}{w}dw=\ln (t)+\ln (u).$

Persamaan (1) membagi integral menjadi dua bagian, sementara (2) mengubah variabel Templat:Math menjadi Templat:Math. Pada ilustrasi dibawah, pembagian integral tersebut dapat disamakan dengan pembagian luasnya menjadi bagian berwarna kuning dan biru. Dengan mengukur luas berwarna biru kembali secara vertikal melalui faktor Templat:Mvar dan menyusutnya melalui faktor yang sama secara horizontal tidak mengubah ukuran luasnya. Dengan memindahkan daerah biru ke daerah kuning, luasnya menyesuaikan grafik fungsi Templat:Math lagi. Oleh karena itu, luas biru di sebelah kiri, yang merupakan integral dari fungsi Templat:Math dengan interval dari Templat:Mvar hingga Templat:Mvar sama dengan integral dari fungsi yang sama dengan interval 1 hingga Templat:Mvar. Hal ini membenarkan persamaan  (2) melalui bukti geometri lainnya.

Sebuah bukti visual tentang rumus hasil kali dari logaritma natural

Rumus pangkat Templat:Math dapat real dalam cara yang serupa:

$\ln (t^r)=\underset{1}{\overset{t^r}{\int }}\frac{1}{x}dx=\underset{1}{\overset{t}{\int }}\frac{1}{w^r}\left(r{w}^{r-1}dw\right)=r\underset{1}{\overset{t}{\int }}\frac{1}{w}dw=r\ln (t).$

Persamaan kedua menggunakan perubahan variabel Templat:Math melalui integral substitusi.

Jumlah keseluruhan timbal balik dari bilangan asli yang dirumuskan

$1+\frac{1}{2}+\frac{1}{3}+\cdots +\frac{1}{n}=\sum _{k=1}^n\frac{1}{k},$

disebut deret harmonik. Deret ini sangat terkait erat dengan logaritma alami, yang dinyatakan melalui pernyataan berikut: ketika Templat:Mvar cenderung menuju takhingga, selisih dari

$\sum _{k=1}^n\frac{1}{k}-\ln (n),$

konvergen (yakni mendekati dengan sembarang) ke sebuah bilangan yang dikenal sebagai konstanta Euler–Mascheroni Templat:Math. Kaitan antara deret harmonik dan logaritma natural membantu dalam menganalisis kinerja algoritma seperti quicksort.

Transendensi logaritma

Bilangan real yang bukan merupakan bilangan aljabar disebut bilangan transendental. Sebagai contoh, Templat:Math dan Templat:Math adalah bilangan transendental, sedangkan $\sqrt{2-\sqrt{3}}$ bukan. Hampir semua bilangan real adalah transendental. Logaritma merupakan sebuah contoh fungsi transendental. Teorema Gelfond–Schneider mengatakan bahwa logaritma biasanya memberikan nilai transendental.

Perhitungan

Tombol logaritma (LOG sebagai bilangan pokok 10 dan LN sebagai bilangan pokok Templat:Mvar) pada sebuah kalkulator grafik TI-83 Plus.

Logaritma merupakan alat hitung yang mudah pada beberapa kasus, seperti Templat:Math. Logaritma pada umumnya dapat dihitung melalui deret kuasa atau rata-rata aritmetika–geometrik, atau didapatkan kembali dari tabel logaritma (sebelum adanya perhitungan logaritma) yang menyediakan ketepatan nilai konstan. Metode Newton, sebuah metode berulang yang menyelesaikan persamaan melalui hampiran, juga dapat dipakai untuk menghitung logaritma, karena fungsi inversnya (yaitu fungsi eksponensial), dapat dihitung dengan cepat. Dengan melihat tabel logaritma, metode yang mirip dengan CORDIC dapat dipakai untuk menghitung logaritma hanya dengan menggunakan operasi penambahan dan geseran bit. Terlebih lagi, algoritma dari logaritma biner menghitung Templat:Math secara berulang berdasarkan penguadratan Templat:Mvar yang berulang dan menggunakan ekspresi

$2^{}\log \left(x^2\right)=2\cdot {}^2\log |x|.$

Deret pangkat

Deret Taylor

Deret Taylor dari Templat:Math berpusat di Templat:Math. Animasi berikut memperlihatkan 10 hampiran pertama beserta dengan hampiran yang ke-99 dan yang ke-100. Hampiran tersebut tidak konvergen karena melebihi jarak 1 dari pusatnya.

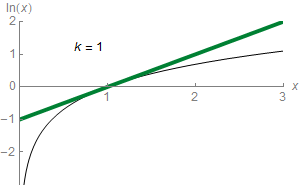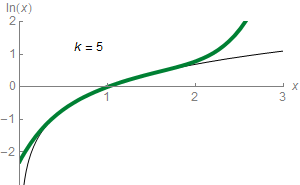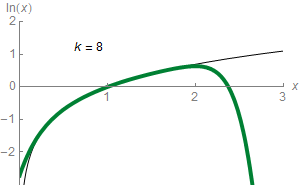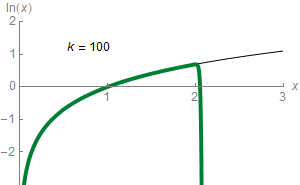
Untuk setiap bilangan Templat:Mvar yang memenuhi sifat Templat:Math, maka berlaku rumus:Templat:Refn

$\begin{array}{cc}\ln (z)& =\frac{(z-1{)}^1}{1}-\frac{(z-1{)}^2}{2}+\frac{(z-1{)}^3}{3}-\frac{(z-1{)}^4}{4}+\cdots \\ & =\sum _{k=1}^{\mathrm{\infty }}(-1{)}^{k+1}\frac{(z-1{)}^k}{k}\end{array}$

Pernyataan di atas merupakan tulisan singkat untuk mengatakan bahwa Templat:Math dapat diaproksimasi sebagai bilangan yang lebih-lebih akurat lagi melalui ekspresi berikut:

$\begin{array}{ccc}(z-1)& & \\ (z-1)& -& \frac{(z-1{)}^2}{2}& \\ (z-1)& -& \frac{(z-1{)}^2}{2}& +& \frac{(z-1{)}^3}{3}\\ ⋮& \end{array}$

Sebagai contoh, pendekatan ketiga saat Templat:Math memberikan nilai 0,4167. Nilai tersebut kira-kira 0,011 lebih besar dari Templat:Math. Deret ini yang mengaproksimasi Templat:Math dengan ketepatan nilai sembarang, menyediakan jumlah dari nilai yang dijumlahkan cukup besar. Dalam kalkulus elementer, Templat:Math adalah limit dari deret ini dan juga merupakan deret Taylor dari logaritma alami di Templat:Math. Deret Taylor dari Templat:Math khususnya menyediakan alat yang berguna untuk mengaproksimasi Templat:Math ketika Templat:Mvar bernilai kecil, Templat:Math:

$\ln (1+z)=z-\frac{z^2}{2}+\frac{z^3}{3}\cdots \approx z.$

Sebagai contoh, hampiran orde pertama memberikan nilai hampiran Templat:Math ketika Templat:Math, yang galatnya 5% lebih kecil dari nilai eksak 0,0953.

Deret lebih efisien

Deret lainnya berasal dari fungsi tangen hiperbolik invers:

$\ln (z)=2\cdot \mathrm{artanh}\frac{z-1}{z+1}=2(\frac{z-1}{z+1}+\frac{1}{3}{\left(\frac{z-1}{z+1}\right)}^3+\frac{1}{5}{\left(\frac{z-1}{z+1}\right)}^5+\cdots ),$

untuk setiap bilangan real Templat:Math.Templat:Refn Dengan menggunakan notasi Sigma, ruas kanan pada rumus di atas juga dapat ditulis sebagai

$\ln (z)=2\sum _{k=0}^{\mathrm{\infty }}\frac{1}{2k+1}{\left(\frac{z-1}{z+1}\right)}^{2k+1}.$

Deret ini dapat diturunkan dari deret Taylor di atas, yang konvergen lebih cepat daripada deret Taylor, khususnya jika Templat:Mvar mendekati 1. Sebagai contoh, untuk Templat:Math, tiga suku pertama dari deret kedua memberikan nilai hampiran Templat:Math dengan galatnya sekitar Templat:Val. Kekonvergenan cepat untuk Templat:Mvar yang mendekati 1 dapat dimanfaatkan sebagai berikut: diberikan sebuah hampiran dengan tingkat akurat yang rendah Templat:Math dan memasukkan ke rumus

$A=\frac{z}{\exp (y)},$

maka logaritma dari Templat:Mvar dirumuskan:

$\ln (z)=y+\ln (A).$

Hampiran awalan Templat:Mvar yang lebih baik adalah dengan membuat nilai Templat:Mvar mendekati ke 1, sehingga nilai logaritma dapat dihitung lebih efisien. Nilai Templat:Mvar dapat dihitung melalui deret eksponensial sehingga nilainya konvergen dengan cepat, asalkan nilai Templat:Mvar tidak terlalu besar. Dengan menghitung logaritma dari Templat:Mvar yang lebih besar dapat direduksi menjadi nilai Templat:Mvar yang lebih kecil dengan menulis Templat:Math, sehingga Templat:Math.

Terdapat metode yang sangat berkaitan dengannya dapat dipakai untuk menghitung logaritma dari bilangan bulat. Dengan memasukkan $z=\frac{n+1}{n}$ pada deret di atas, maka deret tersebut dapat ditulis sebagai berikut:

$\ln (n+1)=\ln (n)+2\sum _{k=0}^{\mathrm{\infty }}\frac{1}{2k+1}{\left(\frac{1}{2n+1}\right)}^{2k+1}.$

Jika diketahui logaritma dari suatu bilangan bulat  Templat:Mvar yang lebih besar, maka deret tersebut menghasilkan sebauah deret yang konvergen dengan cepat untuk Templat:Math, dengan laju konvergensi dari ${\left(\frac{1}{2n+1}\right)}^2$.

Hampiran purata aritmetika-geometrik

Purata aritmetika–geometrik atau rata-rata aritmetika–geometrik menghasilkan hampiran dari logaritma natural dengan tingkatan ketepatan yang tinggi. Pada tahun 1982, Sasaki dan Kanada memperlihatkan bahwa purata ini sangat cepat untuk ketepatan di antara 400 dan 1000 letak desimal, sementara metode deret Taylor biasanya lebih cepat ketika membutuhkan nilai yang kurang akurat. Dalam karyanya, Templat:Math kira-kira sama dengan ketepatan dari Templat:Math (atau Templat:Mvar bit yang tepat) melalui rumus berikut (karena Carl Friedrich Gauss):

$\ln (x)\approx \frac{\pi }{2\mathrm{M}(1,2^{2-m}/x)}-m\ln (2).$

Notasi Templat:Math menyatakan rata-rata aritmetika–geometrik dari Templat:Mvar dan Templat:Mvar. Purata ini didapatkan dengan menghitung rerata Templat:Math (purata aritmetika) dan $\sqrt{xy}$ (purata geometrik) dari Templat:Mvar dan Templat:Mvar secara berulang, lalu misalkan kedua bilangan tersebut merupakan bilangan Templat:Mvar dan Templat:Mvar selanjutnya. Kedua bilangan tersebut konvergen dengan cepat menuju ke limit yang sama, yaitu Templat:Math. Agar pasti bahwa nilai yang diperlukan tepat, maka pilih Templat:Mvar sehingga

$x{2}^m>2^{p/2}.$

Bilangan Templat:Mvar yang lebih besar membuat perhitungan Templat:Math, dengan nilai awal Templat:Mvar dan Templat:Mvar yang merupakan nilai yang sangat jauh, mengambil langkah lebih lanjut agar nilainya konvergen, tetapi memberikan nilai yang lebih tepat. Konstanta seperti Templat:Math dan Templat:Math dapat dihitung melalui deret yang konvergen dengan cepat.

Algoritma Feynman

Richard Feynman, yang mengerjakan proyek Manhattan di Los Alamos National Laboratory, mengembangkan sebuah algoritma pengolahan bit untuk menghitung nilai logaritma. Algoritma tersebut menyerupai pembagian panjang, dan kemudian dipakai dalam sebuah anggota dari rangkaian subkomputer, Connection Machine. Bahkan bahwa setiap bilangan real Templat:Math yang dapat direpresentasikan sebagai hasil kali dari faktor yang berbeda dari bentuk Templat:Math, dipakai dalam algoritma ini. Algoritma ini dibangun secara berurutan bahwa hasil kali Templat:Mvar, yang dimulai dengan Templat:Math dan Templat:Math, mengatakan bahwa jika Templat:Math, maka Templat:Mvar berubah menjadi Templat:Math, sehingga membuat nilai $k$ menaik. Algoritma tersebut berhenti ketika Templat:Mvar cukup besar memberikan nilai akurat yang diinginkan. Karena Templat:Math adalah jumlah dari suku berbentuk Templat:Math yang berpadanan dengan nilai Templat:Mvar dan faktor Templat:Math adalah hasil kali dari  Templat:Mvar, maka Templat:Math dapat dihitung melalui operasi penambahan yang sederhana, yaitu menggunakan tabel dari Templat:Math untuk semua Templat:Mvar. Setiap bilangan pokok dapat dipakai untuk tabel logaritma.

Penerapan

Sebuah cangkang nautilus yang menampilkan bentuk spiral logaritmik.

Logaritma memiliki banyak penerapan di dalam maupun di luar matematika. Ada beberapa kejadian penerapan logaritma yang berkaitan dengan gagasan kekararan skala. Sebagai contoh, setiap ruangan yang terdapat di dalam sebuah cangkang nautilus memiliki kira-kira sama dengan jumlah salinan dari ruang selanjutnya, yang ditimbang melalui faktor konstanta. Contoh tersebut menyerupai bentuk spiral logaritmik. Hukum Benford mengenai distribusi dari angka yang ditunjuk juga dapat dijelaskan melalui kekeraran skala. Logaritma juga berkaitan dengan benda yang memiliki kemiripan terhadap diri sendiri. Sebagai contoh, logaritma muncul dalam analisis tentang algoritma yang menyelesaikan masalah dengan membaginya menjadi dua masalah lebih kecil yang serupa dan memotong kecil penyelesaiannya. Dimensi dari bentuk geometrik menyerupai diri sendiri, dalam artian bahwa bentuk yang bagiannya menyerupai gambarnya secara keseluruhan juga dirumuskan melalui logaritma. Skala logaritmik berguna untuk mengukur perubahan relatif nilai daripada selisih mutlaknya. Terlebih lagi, karena fungsi logaritmik Templat:Math menaik sangat lambat untuk nilai besarTemplat:Mvar, skala logaritmik biasanya menekan data ilmiah yang berskala besar. Logaritma juga muncul dalam rumus ilmiah numerik, seperti persamaan roket Tsiolkovsky, persamaan Fenske, atau persamaan Nernst.

Penerapannya dalam skala logaritmik

Grafik logaritma memperlihatkan kenaikan harga mata uang goldmark di Papiermark selama berlangsungnya hiperinflasi di Jerman pada tahun 1920-an

Satuan kuantitas dalam ilmiah seringkali dinyatakan sebagai logaritma dari kuantitas lain, dengan menggunakan skala logaritmik. Sebagai contoh, desibel merupakan satuan pengukuran yang dikaitkan dengan perhitungan dari kuantitas skala logaritmik. Penguat desibel memberikan 10 kalinya logaritma biasa dari rasio daya atau 20 kalinya logaritma biasa dari rasio tegangan. Satuan inilah yang dipakai untuk mengukur rugi tingkatan ketegangan saat mentransmisi sinyal elektrik, yang bertujuan untuk menjelaskan tingkatan kekuatan aras daya suara dalam akustik, serta mengukur penyerapan cahaya dalam bidang spektrometri dan optika. Selain itu, desibel juga dipakai dalam nisbah sinyal-derau yang menjelaskan seberapa banyak derau dibandingkan dengan sinyal yang berguna. Mirip dengan tadi, nisbah puncak sinyal-derau biasanya dipakai menilai kualitas suara dan metode pemampatan citra melalui logaritma.

Kekuatan gempa bumi diukur dengan mengambil logaritma umum dari energi yang dipancarkan saat terjadinya gempa dalam satuan skala magnitudo momen atau skala magnitudo Ritcher. Sebagai contoh, gempa berkekuatan 5,0 melepaskan 32 kali Templat:Math dan gempa berkekuatan 6,0 melepaskan 1000 kaliTemplat:Math energi berkekuatan 4,0. Skala logaritmik juga dipakai dalam magnitudo kentara untuk mengukur kecerahan bintang. Dalam kimia, negatif dari logaritma desimal, yang disebut sebagai Templat:Vanchor desimal, ditunjukkan dengan huruf "p". Sebagai contoh, pH merupakan kologaritma desimal dari keaktifan dari ion berbentuk hidrogen Templat:Chem yang terbentuk dari air, hidronium. Keaktifan dari ion hidronium dalam air yang netral bernilai 10⁻⁷ mol·L⁻¹, sehingga nilai pH adalah 7. Contoh lainnya, nilai pH dari asam cuka biasanya sekitar 3. Perbedaan nilai sebesar 4 sesuai dengan rasio 10⁴ berdasarkan aktivitasnya, yaitu nilai dari aktivitas ion hidronium cuka sekitar 10⁻³ mol·L⁻¹.

Konsep skala logaritmik dapat dipakai dalam grafik (log-linear) semilog bertujuan untuk memberikan visual terkait satu sumbu, yang biasanya berupa sumbu vertikal, diukur menggunakan perhitungan logaritma. Contohnya seperti grafik disamping menjelaskan nilai yang menaik dengan tajam dari 1 juta hingga 1 triliun ke dalam ruang yang sama (pada sumbu vertikal) saat grafiknya menaik dari 1 hingga 1 juta. Pada grafik tersebut, fungsi eksponensial Templat:Math muncul sebagai garis lurus dengan kemiringan yang sama dengan logaritma dari Templat:Mvar. Selain itu, skala logaritma yang dapat dipakai dalam grafik log-log untuk mengukur sumbu vertikal dan horizontal, sehingga menyebabkan fungsi Templat:Math digambarkan sebagai garis lurus yang mempunyai kemiringan yang sama dengan bilangan yang dipangkat dengan Templat:Mvar, diterapkan pada saat memberikan visual dan menganalisis hukum pangkat.

Penerapannya dalam psikologi

Penerapan logaritma juga terdapat dalam beberapa hukum yang menjelaskan tentang persepsi manusia. Sebagai contoh, hukum Hick menjelaskan kaitan logaritmik antara waktu saat orang mengambil keputusan beserta jumlah keputusan yang dimiliki. Hukum lainnya adalah hukum Fitts, yang memprediksi bahwa waktu yang diperlukan saat bergerak ke daerah target dengan cepat sama dengan fungsi logaritmik dari jarak dan ukuran target. Dalam psikofisika, hukum Weber–Fechner mengatakan kaitan logaritmik dengan stimulus dan sensasi yang dirasakan, contohnya seperti saat orang sedang membawa berat benda yang sesungguhnya dengan yang dirasakan. (Namun, "hukum" ini kurang realistis dengan model belakangan ini, seperti hukum perpangkatan Stevens.)

Studi psikologi menemukan bahwa orang yang sedikit mempunyai pemahaman matematika cenderung mengestimasi nilai kuantitas dengan logaritma, atau dengan kata lain, bilangannya ditempatkan pada garis yang tidak ditandai berdasarkan perhitungan logaritma, sehingga 10 yang ditempatkan mendekati 100 dianggap sebagai 100 yang ditempatkan mendekati 1000. Orang yang memiliki pemahaman yang lebih tinggi memandang hal tersebut sebagai linear yang mengestimasi (letak angka 1000 yang berjarak 10 kali lebih jauh) pada beberapa kasus, namun logaritma dipakai pada saat memplot bilangan-bilangan yang sulit untuk diplotkan secara linear.

Penerapannya dalam teori peluang dan statistika

Templat:Multiple image Dalam teori probabilitas, hukum bilangan besar mengatakan bahwa, untuk sebuah mata uang seimbang, ketika jumlah pelemparan koin naik menuju takhingga, maka kesebandingan dari gambar kepala (atau ekor) yang diamati mendekati satu setengah. Fluktuasi dari nilai kesebandingan yang bernilai satu setengah dijelaskan melalui hukum yang menggunakan logaritma, yaitu hukum logaritma teriterasi.

Logaritma muncul pula dalam sebaran log-normal. Ketika logaritma dari variabel acak mempunyai sebaran normal, maka variabel dikatakan mempunyai sebaran log-normal. Sebaran log-normal ditemukan dalam banyak bidang, dengan suatu variabel dibentuk sebagai hasil kali dari banyaknya variabel acak indenpenden bernilai positif. Contohnya seperti dalam mempelajari turbulensi.

Logaritma dipakai untuk menghitung estimasi kemungkinan maksimum dari model statistika parametrik. Fungsi kemungkinan pada model tersebut bergantung setidaknya satu parameter yang harus diestimasi. Nilai maksimum dari fungsi kemungkinan muncul di nilai parameter yang sama sebagai nilai maksimum logaritma kemungkinan (atau disebut log likelihood), karena logaritma merupakan fungsi menaik. Log-likelihood adalah teknik yang memaksimumkan fungsi dengan mudah, khususnya untuk kemungkinan yang dikali mengenai variabel acak independen.

Hukum Benford menjelaskan kemungkinan digit dalam himpunan data yang banyak, contohnya seperti tinggi bangunan. Menurut hukum Benford, kemungkinan bahwa digit desimal pertama suatu item dalam sampel data adalah Templat:Mvar (yang berkisar dari 1 hingga 9) sama dengan Templat:Math, tanpa memperhatikan satuan pengukuran. Jadi, sekitar 30% data dapat diduga mempunyai 1 sebagai digit pertama, 18% dimulai dengan 2, dst. Penyimpangan dari hukum Benford dihitung oleh para akuntan untuk membantu mendeteksi penipuan data akuntansi.

Penerapannya dalam kompleksitas perhitungan

Cabang dalam ilmu komputer yang mempelajari performa dari suatu algoritma dalam menyelesaikan persoalan atau masalah tertentu disebut analisis algoritma. Logaritma sangat penting dalam menjelaskan algoritma tersebut dengan membagi suatu masalah menjadi lebih kecil, serta menghubungkan penyelesaian dari submasalah.

Sebagai contoh, cara algoritma pencarian biner (Templat:Lang-en) dalam mencari bilangan dalam daftar yang tersortir adalah dengan memeriksa entri tengah dan meneruskannya di sebagian sebelum atau sesudah entri tengah jika tidak ditemukan bilangannya. Umumnya, algoritma ini memerlukan perbandingan Templat:Math, dengan Templat:Mvar adalah panjang daftar. Mirip dengan sebelumnya, algoritma urut gabungan menyortir daftar yang belum tersortir dengan membagi daftar menjadi setengah bagian dan mengurutkan daftar-daftar tersebut dahulu sebelum menggabungkan hasilnya. Algoritma urut gabungan biasanya memerlukan waktu yang kira-kira sebanding dengan Templat:Math. Bilangan pokok logaritma tidak dijelaskan secara spesifik, karena hasilnya hanya berubah oleh faktor konstanta saat ada bilangan pokok lain yang sedang dipakai. Faktor konstanta biasanya diabaikan dalam analisis algoritma dalam model biaya seragam (Templat:Lang-en) yang standar.

Suatu fungsi Templat:Math dikatakan bertumbuh secara logaritmik jika Templat:Math (setidaknya atau kira-kira) sebanding dengan logaritma dari Templat:Mvar, namun istilah ini dipakai sebagai fungsi eksponensial dalam menjelaskan pertumbuhan organisme secara biologis. Sebagai contoh, setiap bilangan asli Templat:Mvar dapat direpresentasikan dalam bentuk bilangan biner yang tidak lebih dari Templat:Math bit. Dengan kata lain, jumlah memori diperlukan untuk menyimpan Templat:Mvar pertumbuhan secara logaritmik dengan Templat:Mvar.

Penerapannya dalam entropi dan ketidakteraturan

Bola biliar di atas meja biliar oval. Dua partikel yang bermula pada pusat meja dengan sudut luncur yang berbeda satu derajat, akan memiliki jalur yang amat berbeda karena pemantulan pada pinggir meja biliar

Entropi secara umum adalah ukuran dari ketidakteraturan dari suatu sistem. Dalam termodinamika statistik, sebuah entropi, disimbolkan dengan Templat:Math, dari sebuah sistem, didefinisikan dengan:

$S=-k\sum _i{p}_i\ln (p_i).$

Hasilnya adalah seluruh kondisi Templat:Mvar yang mungkin dari sistem yang dimaksud, contoh posisi dari partikel gas di dalam sebuah tangki. Lebih lanjut lagi, Templat:Math adalah kemungkinan bahwa kondisi Templat:Mvar telah tercapai dan Templat:Mvar adalah konstanta Boltzmann. Sama halnya dengan entropi dalam teori informasi yang mengukur kuantitas dari informasi. Jika penerima pesan mengharapkan sejumlah Templat:Mvar pesan yang mungkin diterima dengan besar kemungkinan masing-masing yang setara, maka sejumlah informasi yang tersampaikan oleh pesan tersebut dapat dikuantifikasi dengan bit Templat:Math.

Eksponen Lyapunov menggunakan logaritma untuk mengukur derajat ketidakteraturan dari sistem yang dinamis. Contoh partikel yang bergerak di meja biliar oval, di mana bahkan perubahan sekecil apapun dari kondisi awal dapat memberikan hasil, yaitu jalur yang dilalui, yang sangat berbeda. Sistem yang dimaksud disebut dengan kekacauan di dalam sistem deterministik karena galat yang kecil namun terukur dari kondisi awal dapat diprediksi akan memberikan hasil akhir yang sangat berbeda. Setidaknya satu eksponen Lyapunov dari sistem kekacauan yang deterministik akan bernilai positif.

Penerapannya dalam bangunan fraktal

Segitiga Sierpinski (di sebelah kanan) dibangun dengan menggantikan segitiga sama sisi secara berulang dengan tiga salinan dirinya yang lebih kecil.

Logaritma muncul dalam definiisi dimensi fraktal. Fraktal merupakan benda-benda geometri yang menyerupai dirinya, dalam artian bahwa benda geometri tersebut mereproduksi dirinya lebih kecil, penjelasan kasarnya, di seluruh strukturnya. Contohnya seperti segitiga Sierpiński, dengan dimensi Hausdorffnya adalah Templat:Math, dapat diliputi dengan tiga salinan dirinya, masing-masing sisinya dibagi menjadi setengah dari panjang awalnya. Adapula gagasan dimensi fraktal berdasarkan logaritma lainnya diperoleh dengan menghitung jumlah kotak yang diperlukan untuk meliputi frakal dalam himpunan.

Penerapannya dalam musik

Logaritma berkaitan dengan bunyi nada dan interval dalam musik. Dalam temperamen sama, perbandingan frekuensi bergantung pada interval di antara dua nada saja, bukan pada frekuensi yang spesifik atau tinggi dari nada tunggal. Sebagai contoh, nada A mempunyai frekuensi 440 Hz dan B-flat mempunyai frekuensi 466 Hz. Interval antara nada A dengan B-flat ini digolongkan sebagai semi-nada, karena intervalnya berada di antara B-flat dan B (yang mempunyai frekuensi 493 Hz). Maka, perbandingan frekuensinya adalah:

$\frac{466}{440}\approx \frac{493}{466}\approx 1,059\approx \sqrt[12]{2}.$

Peran logaritma dalam musik dapat dipakai untuk menjelaskan interval berikut: suatu interval diukur dalam semi-nada dengan mengambil logaritma dengan Templat:Nowrap dari perbandingan frekuensi, sedangkan logaritma dengan Templat:Nowrap dari perbandingan frekuensi menyatakan interval dalam sen, ratusan semi-nada. Logaritma yang terakhir dipakai untuk pengodean yang lebih halus, karena diperlukan untuk temperamen tak sama.

Interval (dua bunyi nada yang dimainkan dalam waktu yang sama)	Bunyi nada 1/12 Templat:Audio	Semi-nada Templat:Audio	Just major third Templat:Audio	Major third Templat:Audio	Tritone Templat:Audio	Oktaf Templat:Audio
Rasio frekuensi r	$2^{\frac{1}{72}}\approx 1.0097$	$2^{\frac{1}{12}}\approx 1.0595$	$\frac{5}{4}=1.25$	$\begin{array}{cc}{2}^{\frac{4}{12}}& =\sqrt[3]{2}\\ & \approx 1.2599\end{array}$	$\begin{array}{cc}{2}^{\frac{6}{12}}& =\sqrt{2}\\ & \approx 1.4142\end{array}$	$2^{\frac{12}{12}}=2$
Jumlah semi-nada yang sama${\sqrt[12]{2}}^{}\log r=12{}^2\log r$	$\frac{1}{6}$	$1$	$\approx 3,8631$	$4$	$6$	$12$
Jumlah sen yang sama${\sqrt[1200]{2}}^{}\log r=1200{}^2\log r$	$16\frac{2}{3}$	$100$	$\approx 386,31$	$400$	$600$	$1200$

Penerapannya dalam teori bilangan

Logaritma alami sangat berkaitan dengan salah satu topik dalam teori bilangan, yaitu menghitung bilangan prima. Untuk setiap bilangan bulat Templat:Mvar, jumlah bilangan prima kurang dari sama dengan Templat:Mvar dinyatakan sebagai Templat:Math. Teorema bilangan prima mengatakan bahwa Templat:Math kira-kira sama dengan

$\frac{x}{\ln (x)},$

yang berarti bahwa fungsi pencacahan bilangan prima kira-kira sama dengan perbandingan dari Templat:Math dan pecahan yang mendekati 1 ketika Templat:Mvar menuju ke takhingga. Akibatnya, peluang dari bilangan yang dipilih secara acak di antara 1 dan Templat:Mvar adalah bilangan prima berbanding terbalik dengan jumlah digit desimal Templat:Mvar. Pendekatan Templat:Math yang lebih baik merupakan fungsi integral Euler Templat:Math, yang didefinisikan sebagai

$\mathrm{L}\mathrm{i}(x)=\underset{2}{\overset{x}{\int }}\frac{1}{\ln (t)}dt.$

Hipotesis Riemann, yang merupakan salah satu konjektur matemtika terbuka yang paling terlama, dapat dinyatakan dalam bentuk perbandingan Templat:Math dan Templat:Math. Teorema Erdős–Kac mengatakan bahwa jumlah faktor bilangan prima yang berbeda juga melibatkan logaritma alami.

Logaritma dari n faktorial, Templat:Math, dirumuskan sebagai

$\ln (n!)=\ln (1)+\ln (2)+\cdots +\ln (n).$

Rumus di atas dapat dipakai utnuk memperoleh sebuah hampiran dari Templat:Math untuk setiap bilangan Templat:Mvar yang lebih besar, yaitu rumus Stirling.

Perumuman

Logaritma kompleks

Templat:Main Semua bilangan kompleks Templat:Mvar yang menyelesaikan persamaan

$e^a=z$

disebut logaritma kompleks dari Templat:Mvar, ketika Templat:Mvar (dianggap sebagai) bilangan kompleks. Bilangan kompleks biasanya dinyatakan sebagai Templat:Math, dengan Templat:Mvar dan Templat:Mvar adalah bilangan real dan Templat:Mvar adalah satuan imajiner (satuan yang dikuadratkan memberikan nilai −1). Bilangan kompleks dapat divisualisasikan melalui sebuah titik dalam bidang kompleks, seperti yang diperlihatkan pada gambar berikut. Bentuk polar menulis bilangan kompleks tak-nol Templat:Mvar melalui titik nilai mutlak, yang berarti jarak yang berupa bilangan bernilai real dan positif Templat:Mvar sama dengan titik Templat:Mvar ke titik asalnya. Bentuk polar juga menulis sebuah sudut antara bilangan real pada sumbu-Templat:Math (yakni sumbu-Templat:Mvar)  Templat:Math dan garis yang melalui titik asal dan titik Templat:Mvar. Sudut tersebut disebut sebagai argumen dari Templat:Mvar.

Bentuk polar dari Templat:Math. Templat:Mvar dan Templat:Mvar adalah argumen dari Templat:Mvar.

Nilai mutlak Templat:Mvar dari Templat:Mvar dinyatakan sebagai

$r=\sqrt{x^2+y^2}.$

Dengan menggunakan pandangan geometris pada fungsi sinus dan kosinus beserta periodisitasnya dalam Templat:Math, setiap bilangan kompleks Templat:Mvar dapat dinyatakan sebagai

$z=x+iy=r(\cos \phi +i\sin \phi )=r(\cos (\phi +2k\pi )+i\sin (\phi +2k\pi )),$

untuk setiap bilangan bulat Templat:Mvar. Nyatanya, argumen dari Templat:Mvar tidak dijelaskan secara unik, yakni: bilangan Templat:Mvar dan Templat:Math adalah argumen valid dari Templat:Mvar untuk semua bilangan bulat Templat:Mvar, karena menambahkan Templat:Math radian atau k⋅360°Templat:Refn ke bilangan Templat:Mvar berpadanan dengan "lilitan" di sekitar titik asal yang berputar berlawanan arah jarum jam sebanyak Templat:Mvar putaran. Hasil bilangan kompleks selalu Templat:Mvar, seperti yang diilustrasikan pada gambar untuk Templat:Math. Setidaknya ada salah satu dari argumen Templat:Mvar yang mungkin disebut sebagai argumen prinsip, yang dilambangkan Templat:Math, dipilih dengan memerlukan putaran Templat:Mvar di selang Templat:Open-closed atau Templat:Math. Daerah-daerah tersebut, dengan argumen Templat:Mvar ditentukan sekali disebut cabang dari fungsi argumen.

Rumus Euler mengaitkan fungsi trigonometri sinus dan kosinus dengan eksponensial kompleks:

$e^{i\phi }=\cos \phi +i\sin \phi .$

Dengan menggunakan rumus di atas, dan periodisitasnya lagi, maka berlaku identitas berikut:

$\begin{array}{ccc}z& =& r(\cos \phi +i\sin \phi )\\ & =& r(\cos (\phi +2k\pi )+i\sin (\phi +2k\pi ))\\ & =& r{e}^{i(\phi +2k\pi )}\\ & =& e^{\ln (r)}{e}^{i(\phi +2k\pi )}\\ & =& e^{\ln (r)+i(\phi +2k\pi )}=e^{a_k},\end{array}$

dengan Templat:Math adalah fungsi logaritma real tunggal, Templat:Math menyatakan logaritma kompleks dari Templat:Mvar, dan Templat:Mvar bilangan bulat sembarang. Karena itu, logaritma kompleks dari Templat:Mvar, yang semua bilangan kompleks Templat:Math untuk Templat:Mvar pangkat Templat:Math sama dengan Templat:Mvar, mempunyai tak berhingga banyaknya nilai

$a_k=\ln (r)+i(\phi +2k\pi ),$ untuk bilangan bulat sembarang Templat:Mvar.

Cabang prinsip (-Templat:Pi, Templat:Pi) dari prinsip logaritma kompleks, Templat:Math. Titik berwarna hitam di Templat:Math berpadanan dengan nilai titik nol dan warna yang lebih cerah mengacu pada nilai mutlak lebih besar. Rona dari warna mengkodekan argumen dari Templat:Math.

Dengan mengambil Templat:Mvar sehingga Templat:Math ada di dalam selang yang ditentukan untuk argumen prinsip, maka Templat:Math disebut nilai prinsip dari logaritma, dinotasikan sebagai Templat:Math. Argumen prinsip setiap bilangan real positif  Templat:Mvar bernilai 0, jadi Templat:Math adalah sebuah bilangan real yang sama dengan logaritma (alami). Akan tetapi, rumus logaritma tentang darab dan perpangkatan bilangan di atas tidak memberikan perumuman terkait nilai prinsip dari logaritma kompleks.

Ilustrasi tersebut menggambarkan Templat:Math, membatasi argumen Templat:Mvar dengan interval Templat:Open-closed. Cara memadankan cabang dari logaritma kompleks mempunyai ketakkontinuan di sepanjang sumbu-Templat:Mvar real negatif, seperti yang dapat dilihat pada lompatan hue di gambar. Saat melintasi batas, ketakkontinuan tersebut dimulai dari lompatan hingga batas lain yang ada di cabang yang sama, dalam artian bahwa tiada perubahan dengan nilai-Templat:Mvar dari cabang tetangga kontinu yang berpadanan. Lokus tersebut dinamakan potongan cabang. Dengan menghapus perbatasan argumen, maka relasi "argumen dari Templat:Mvar" dan "logaritma dari Templat:Mvar" menjadi fungsi bernilai banyak.

Kebalikan dari fungsi eksponensial lainnya

Eksponensiasi muncul dalam cabang matematika dan fungsi inversnya seringkali mengacu pada logaritma. Sebagai contoh, logaritma matriks merupakan fungsi invers (bernilai banyak) dari eksponensial matriks. Contohnya lain seperti fungsi logaritma p-adic, fungsi invers dari fungsi eksponensial p-adic. Kedua fungsi tersebut didefinisikan melalui deret Taylor yang analog dengan kasus bilangan real. Dalam konteks geometri diferensial, peta eksponensial memetakan ruang garis singgung di sebuah titik lipatan ke lingkungan titik tersebut. Kebalikannya juga disebut peta logaritma.

Dalam konteks grup hingga, eksponensiasi dinyatakan dengan mengalikan satu anggota grup Templat:Mvar dengan dirinya secara berulang. Logaritma diskret merupakan bilangan bulat Templat:Mvar yang menyelesaikan persamaan

$b^n=x,$

dengan Templat:Mvar adalah anggota dari grup. Mengerjakan solusi eksponensiasi dapat dilakukan dengan efisien, namun logaritma diskret dipercayai bahwa sangat sulit untuk menghitungnya dalam beberapa grup. Asimetri dari grup tersebut mempunyai penerapan penting dalam kriptografi kunci publik, contohnya seperti pertukaran kunci Diffie–Hellman, sebuah pertukaran kunci sehari-hari yang memungkinkan pertukaran kunci kriptografi terhadap saluran informasi yang tidak diamankan. Logaritma Zech berkaitan dengan logaritma diskret dalam grup perkalian anggota taknol dari medan hingga.

Templat:AnchorAdapun fungsi invers berupa logaritma lainnya. Fungsi tersebut di antaranya: logaritma ganda Templat:Math yang merupakan kebalikan dari fungsi eksponensial ganda, superlogaritma yang merupakan kebalikan dari tetrasi, fungsi Lambert W yang merupakan kebalikan dari fungsi Templat:Math, dan logit yang merupakan kebalikan dari fungsi logistik.

Konsep yang berkaitan

Berdasarkan sudut pandang teori grup, identitas Templat:Math menyatakan isomorfisme grup antara bilangan riil positif terhadap perkalian bilangan riil positif terhadap penambahan. Fungsi logaritmik hanya isomorfisme kontinu antara grup. Berdasarkan pengertian isomorfisme tersebut, ukuran Haar (ukuran Lebesgue) Templat:Math pada riil berpadanan dengan ukuran Haar Templat:Math pada bilangan real positif. Bilangan riil taknegatif tidak hanya terhadap operasi perkalian, namun juga terhadap operasi penambahan, dan bilangan riil taknegatif membentuk semigelanggang, yang disebut sebagai semigelanggang probabilitas, bahkan membentuk semigelanggang. Maka logaritma yang mengambil perkalian dengan penambahan (perkalian logaritma), dan mengambil penambahan dengan penambahan logaritma, memberikan isomorfisme semigelanggang di antara semigelanggang probabilitas dan semigelanggang logaritma.

Konsep ini juga terdapat di dalam analisis kompleks dan geometri aljabar, yang logaritmik satu bentuk Templat:Math adalah bentuk diferensial dengan pole logaritmik.

Selain itu, terdapat polilogaritma, sebuah fungsi yang didefinisikan sebagai

${\mathrm{Li}}_s(z)=\sum _{k=1}^{\mathrm{\infty }}\frac{z^k}{k^s}.$

Fungsi ini mempunyai kaitan dengan logaritma alami dengan Templat:Math. Terlebih lagi, ketika Templat:Math, nilai dari Templat:Math sama dengan fungsi zeta Riemann, yang dinyatakan sebagai Templat:Math.

Lihat pula

• Eksponen desimal (dex)
• Fungsi eksponensial
• Indeks artikel logaritma
• Notasi logaritmik

Pranala luar

• Templat:Commons category-inline
• Templat:Wiktionary-inline
• Templat:Sister-inline
• Templat:MathWorld
• Khan Academy: Logarithms, free online micro lectures
• Templat:Springer
• Templat:Citation
• Templat:Citation
• Templat:Cite EB1911