Lapangan (matematika)

Templat:Struktur aljabar Templat:Sidebar with collapsible lists Lapangan atau medan (juga disebut bidang) dalam matematika adalah suatu struktur aljabar dengan operasi seperti penambahan, pengurangan, perkalian, dan pembagian yang memenuhi aksioma tertentu. Lapangan yang kerap kali dijumpai adalah lapangan bilangan riil, lapangan bilangan kompleks dan bilangan rasional.

Medan yang paling dikenal adalah medan bilangan rasional, bidang bilangan riil dan medan bilangan kompleks. Terdapat medan lainnya, seperti medan fungsi rasional, medan fungsi aljabar, medan bilangan aljabar, dan Medan p-adik umumnya digunakan dan dipelajari dalam matematika, terutama dalam teori bilangan dan geometri aljabar. Sebagian besar protokol kriptografi mengandalkan Medan hingga, yaitu bidang dengan banyak elemen.

Relasi dua medan diekspresikan dengan gagasan tentang ekstensi medan. Teori Galois yang diprakarsai oleh Évariste Galois pada tahun 1830-an, dikhususkan untuk memahami kesimetrian perluasan medan. Di antara hasil lainnya, teori ini menunjukkan bahwa segitiga tiga sudut dan mengkuadratkan lingkaran tidak dapat dilakukan dengan kompas dan garis lurus. Selain itu, ini menunjukkan bahwa persamaan kuintik, secara umum, tidak berpenyelesaian secara aljabar.

Medan berfungsi sebagai gagasan dasar dalam beberapa ranah matematika. Ini mencakup berbagai cabang analisis matematika yang didasarkan pada medan dengan struktur tambahan. Teorema dasar dalam analisis bergantung pada sifat struktural medan bilangan riil. Yang terpenting untuk tujuan aljabar, medan yang digunakan sebagai skalar untuk ruang vektor, yang merupakan konteks umum standar untuk aljabar linear. Medan bilangan bagian dari medan bilangan rasional, dipelajari secara mendalam di teori bilangan. Medan fungsi dapat membantu mendeskripsikan sifat objek geometris.

Definisi

Contoh sebuah lapangan adalah himpunan bilangan rasional Q. Dalam Q terdapat empat operasi dasar: penjumlahan bersama dengan pengurangan, dan perkalian dengan pembagian. Secara intuitif, suatu lapangan adalah himpunan bilangan yang memiliki empat operasi seperti itu. Agar memenuhi syarat sebagai lapangan, operasi-operasi tersebut harus memenuhi aksioma tertentu.

Sebuah lapangan adalah sebuah himpunan, misalkan dinamakan F, bersama dengan dua operasi biner, yang biasanya dinamakan sebagai penambahan dan perkalian, masing-masing dilambangkan sebagai + dan ·, sehingga aksioma berikut berlaku:

Tertutup terhadap penambahan dan perkalian: Untuk semua a, b anggota F, baik a + b dan a · b ada dalam F (atau, dengan rumusan lebih formal, + dan . adalah operasi biner terhadap F).
Sifat asosiatif penambahan dan perkalian: Untuk semua a, b, and c dalam F, persamaan berikut berlaku: Templat:Nowrap begina + (b + c) = (a + b) + cTemplat:Nowrap end dan Templat:Nowrap begina · (b · c) = (a · b) · cTemplat:Nowrap end.
Sifat komutatif penjumlahan dan perkalian: Untuk semua a dan b dalam F, kesamaan berikut berlaku: Templat:Nowrap begina + b = b + aTemplat:Nowrap end dan Templat:Nowrap begina · b = b · aTemplat:Nowrap end.
Unsur identitas dalam penambahan dan perkalian: Terdapat anggota atau unsur F, yang dinamakan unsur identitas penambahan yang dilambangkan sebagai 0, sehingga untuk semua a dalam F, Templat:Nowrap begina + 0 = aTemplat:Nowrap end. Begitu pula, terdapat anggota, yang dinamakan sebagai unsur identitas perkalian yang dilambangkan dengan 1, sehingga untuk semua a dalam F, Templat:Nowrap begina · 1 = aTemplat:Nowrap end. Unsur identitas penambahan dan perkalian disyaratkan berbeda, untuk alasan teknis.

Invers penambahan dan perkalian: Untuk setiap a dalam F, terdapat sebuah anggota, -a dalam F, sehingga Templat:Nowrap begina + (−a) = 0Templat:Nowrap end. Dengan cara yang sama, untuk setiap a dalam F selain 0, terdapat anggota a⁻¹ in F,sehingga Templat:Nowrap begina · a⁻¹ = 1Templat:Nowrap end. (Unsur a + (−b) dan a · b⁻¹ masing-masing dinamakan a − b and a/b) Dengan kata lain, terdapat operasi pengurangan dan pembagian.
Sifat distributif perkalian terhadap penjumlahan: Untuk semua a, b dan c dalam F, kesamaan berikut berlaku: Templat:Nowrap begina · (b + c) = (a · b) + (a · c)Templat:Nowrap end.

Contoh

Bilangan rasional

Templat:Main Bilangan rasional telah banyak digunakan jauh sebelum elaborasi konsep lapangan. Itu adalah bilangan yang dapat ditulis sebagai pecahan Templat:Math, dimana Templat:Math dan Templat:Math adalah bilangan bulat, dan Templat:Math. Kebalikan aditif dari pecahan tersebut adalah Templat:Math, dan pembalikan perkalian (asalkan Templat:Math) adalah Templat:Math, yang bisa dilihat sebagai berikut:

\frac{b}{a} \cdot \frac{a}{b} = \frac{b a}{a b} = 1 .

Aksioma bidang yang diperlukan secara abstrak direduksi menjadi sifat standar bilangan rasional. Misalnya hukum distributivitas dapat dibuktikan sebagai berikut:^[1]

\begin{matrix} \frac{a}{b} \cdot (\frac{c}{d} + \frac{e}{f}) \\ = & \frac{a}{b} \cdot (\frac{c}{d} \cdot \frac{f}{f} + \frac{e}{f} \cdot \frac{d}{d}) \\ = & \frac{a}{b} \cdot (\frac{c f}{d f} + \frac{e d}{f d}) = \frac{a}{b} \cdot \frac{c f + e d}{d f} \\ = & \frac{a (c f + e d)}{b d f} = \frac{a c f}{b d f} + \frac{a e d}{b d f} = \frac{a c}{b d} + \frac{a e}{b f} \\ = & \frac{a}{b} \cdot \frac{c}{d} + \frac{a}{b} \cdot \frac{e}{f} . \end{matrix}

Bilangan riil dan kompleks

Templat:Main Bilangan riil Templat:Math, dengan operasi penjumlahan dan perkalian yang biasa, juga membentuk bidang. Bilangan kompleks Templat:Math terdiri dari ekspresi

Templat:Math dengan Templat:Math,

dimana Templat:Math adalah unit imajiner, yaitu bilangan (non-nyata) memuaskan Templat:Math. Penjumlahan dan perkalian bilangan real didefinisikan sedemikian rupa sehingga ekspresi jenis ini memenuhi semua aksioma medan dan karenanya berlaku untuk Templat:Math. Misalnya, penegakan hukum distributif

Templat:Math

Ini langsung bahwa ini lagi-lagi merupakan ekspresi dari tipe di atas, dan bilangan kompleks membentuk bidang. Bilangan kompleks dapat direpresentasikan secara geometris sebagai titik dalam bidang. dengan koordinat kartesius yang diberikan oleh bilangan real dari ekspresi yang mendeskripsikannya, atau sebagai panah dari asal ke titik-titik ini, ditentukan oleh panjangnya dan sudut tertutup dengan beberapa. Penambahan kemudian sesuai dengan penggabungan panah ke jajaran genjang intuitif (menambahkan koordinat Kartesius), dan perkaliannya, kurang intuitif, menggabungkan putaran dan skala panah (menambahkan sudut dan mengalikan panjangnya). Bidang bilangan real dan kompleks digunakan di seluruh matematika, fisika, teknik, statistik, dan banyak disiplin ilmu lainnya.

Bilangan konstruksibel

Templat:Main

Di zaman kuno, beberapa masalah geometris menyangkut kelayakan (dalam) konstruksi bilangan tertentu dengan kompas dan garis lurus. Misalnya, orang Yunani tidak mengetahui bahwa secara umum tidak mungkin untuk membagi dua sudut tertentu dengan cara ini. Masalah ini dapat diselesaikan dengan menggunakan bidang bilangan konstruksibel.^[2] Bilangan konstruktif riil, menurut definisi, adalah panjang segmen garis yang dapat dibangun dari titik 0 dan 1 dalam banyak langkah tak terhingga hanya dengan menggunakan kompas dan garis lurus. Angka-angka ini, diberkahi dengan operasi bidang bilangan real, terbatas pada bilangan yang dapat dibangun, membentuk bidang, yang mencakup bidang Templat:Math of angka rasional. Ilustrasi menunjukkan konstruksi akar kuadrat dari bilangan yang dapat dibangun, tidak harus terkandung di dalamnya Templat:Math. Menggunakan label dalam ilustrasi, buat segmen Templat:Math, Templat:Math, dan setengah lingkaran berakhir Templat:Math (pusatkan di titik tengah Templat:Math), yang memotong garis tegak lurus melalui Templat:Math pada satu titik Templat:Math, pada jarak tepat $h = \sqrt{p}$ dari Templat:Math jika Templat:Math memiliki panjang satu.

Tidak semua bilangan real dapat dibangun. Dapat ditunjukkan bahwa $\sqrt[3]{2}$ bukanlah bilangan yang dapat dibangun, yang menyiratkan bahwa tidak mungkin untuk membangun dengan kompas dan meluruskan panjang sisi sebuah kubus dengan volume 2, masalah lain yang ditimbulkan oleh orang Yunani kuno.

Bidang dengan empat elemen

Penambahan

Perkalian

+	Templat:Math	Templat:Math	Templat:Math	Templat:Math
Templat:Math	Templat:Color	Templat:Color	Templat:Math	Templat:Math
Templat:Math	Templat:Color	Templat:Color	Templat:Math	Templat:Math
Templat:Math	Templat:Math	Templat:Math	Templat:Math	Templat:Math
Templat:Math	Templat:Math	Templat:Math	Templat:Math	Templat:Math

·	Templat:Math	Templat:Math	Templat:Math	Templat:Math
Templat:Math	Templat:Color	Templat:Color	Templat:Math	Templat:Math
Templat:Math	Templat:Color	Templat:Color	Templat:Math	Templat:Math
Templat:Math	Templat:Math	Templat:Math	Templat:Math	Templat:Math
Templat:Math	Templat:Math	Templat:Math	Templat:Math	Templat:Math

Selain sistem bilangan yang sudah dikenal seperti rasio, ada contoh bidang lain yang kurang langsung. Contoh berikut adalah bidang yang terdiri dari empat elemen yang disebut Templat:Math, Templat:Math, Templat:Math, dan Templat:Math. Notasi Templat:Math memainkan peran elemen identitas aditif (dilambangkan 0 dalam aksioma di atas), dan I adalah identitas perkalian (dilambangkan 1 dalam aksioma di atas). Aksioma medan dapat diverifikasi dengan menggunakan beberapa teori medan lagi, atau dengan perhitungan langsung. Sebagai contoh,

Templat:Math, yang sama dengan Templat:Nowrap, seperti yang dipersyaratkan oleh distribusi.

Bidang ini disebut bidang hingga dengan empat elemen, dan dilambangkan Templat:Math or Templat:Math.^[3] Bagian terdiri dari Templat:Math and Templat:Math (disorot dengan warna merah pada tabel di sebelah kanan) juga merupakan bidang, yang dikenal sebagai bidang biner Templat:Math atau Templat:Math. Dalam konteks ilmu komputer dan Aljabar Boolean, Templat:Math dan Templat:Math masing-masing sering dilambangkan dengan false dan true , penambahan kemudian dilambangkan XOR (eksklusif atau), dan perkalian dilambangkan AND. Dengan kata lain, struktur bidang biner adalah struktur dasar yang memungkinkan dilakukannya komputasi dengan bit.

Gagasan dasar

Dalam bagian ini, Templat:Math menunjukkan medan sembarang dan Templat:Math, serta Templat:Math elemen sembarang dari Templat:Math.

Konsekuensi dari definisi

Satu memiliki Templat:Math dan Templat:Math. Secara khusus, seseorang dapat menyimpulkan kebalikan aditif dari setiap elemen segera setelah dia mengetahui Templat:Math.^[1]

Jika Templat:Math kemudian Templat:Math atau Templat:Math harus 0, karena, jika Templat:Math, kemudian Templat:Math. Ini berarti bahwa setiap bidang adalah domain integral.

Selain itu, properti berikut ini berlaku untuk semua elemen Templat:Math dan Templat:Math:

Templat:Math

Aditif dan grup perkalian dari sebuah medan

Aksioma sebuah medan Templat:Math adalah grup abelian di bawah tambahan. Grup ini disebut grup aditif pada bidang, dan terkadang dilambangkan dengan Templat:Math ketika hanya menandai sebagai Templat:Math yang hanya membingungkan.

Demikian pula, elemen bukan nol dari Templat:Math membentuk grup abelian dalam perkalian yang disebut grup perkalian, dan dilambangkan dengan Templat:Math untuk Templat:Math atau Templat:Math.

Medan didefinisikan sebagai himpunan Templat:Math dengan dua operasi yang dilambangkan sebagai penjumlahan dan perkalian sehingga Templat:Math adalah grup abelian dalam penjumlahan, Templat:Math adalah grup abelian dalam perkalian,^{[catatan 1]} dan perkalian adalah distributif di atas penjumlahan.^{[nb 1]} Oleh karena itu, beberapa pernyataan dasar tentang medan diperoleh dengan menerapkan fakta umum grup. Misalnya, penjumlahan dan perkalian inversi Templat:Math dan Templat:Math ditentukan secara unik oleh Templat:Math.

Persyaratan yang mengikuti Templat:Math, karena 1 adalah elemen identitas grup tidak berisi 0.^[4] Jadi, gelanggang trivial yang terdiri dari satu elemen adalah bukan medan.

Setiap subgrup hingga dari grup perkalian sebuah bidang adalah siklik (lihat Templat:Slink).

Karakteristik

Selain perkalian dua elemen F, dimungkinkan untuk mendefinisikan produk Templat:Math dari elemen arbitrer Templat:Math dari Templat:Math dengan bilangan bulat positif Templat:Math sebagai jumlah lipat-Templat:Math

Templat:Math (yang merupakan elemen dari Templat:Math.)

Jika tidak ada bilangan bulat positif, maka

Templat:Math,

maka Templat:Math dikatakan memiliki karakteristik 0.^[5] Misalnya medan bilangan rasional Templat:Math memiliki karakteristik 0 karena tidak ada bilangan bulat positif Templat:Math adalah nol. Sebaliknya, jika adalah bilangan bulat positif Templat:Math yang memenuhi persamaan ini, bilangan bulat positif terkecil dapat ditampilkan sebagai bilangan prima. Biasanya dilambangkan dengan Templat:Math dan kemudian medan dikatakan memiliki karakteristik Templat:Math. Misalnya, medan Templat:Math memiliki karakteristik 2 dalam^{[catatan 2]} Templat:Math.

Jika Templat:Math memiliki karakteristik Templat:Math, maka Templat:Math untuk semua Templat:Math dalam Templat:Math. Ini menjelaskan

Templat:Math,

karena semua koefisien binomial lainnya yang muncul dalam rumus binomial habis dibagi Templat:Math. Maka, Templat:Math (faktor Templat:Math) adalah kuasa-Templat:Math, yaitu, hasil kali lipat-Templat:Math dari elemen Templat:Math. Oleh karena itu, peta Frobenius

Templat:Math

kompatibel dengan penambahan dalam Templat:Math (dan juga dengan perkalian), dan merupakan homomorfisme medan.^[6] Adanya homomorfisme ini membuat medan dengan karakteristik Templat:Math sangat berbeda dengan bidang dengan karakteristik 0.

Submedan dan medan utama

Sebuah submedan Templat:Math dari medan Templat:Math adalah himpunan bagian dari Templat:Math yang merupakan medan yang terkait dengan operasi medan dari Templat:Math. Setara dengan Templat:Math adalah himpunan bagian dari Templat:Math yang merupakan Templat:Math, dan sebagai penutupan dengan penjumlahan, perkalian, aditif invers dan perkalian invers dari elemen bukan nol. Maka Templat:Math, untuk semua Templat:Math kedua Templat:Math dan Templat:Math adalah Templat:Math, dan untuk semua Templat:Math dal5 Templat:Math, kedua Templat:Math dan Templat:Math adalah Templat:Math.

Medan hingga

Templat:Main Medan hingga (juga disebut medan Galois) adalah medan dengan elemen hingga dimana jumlahnya yang disebut sebagai urutan medan. Contoh pengantar di atas Templat:Math adalah medan dengan empat elemen. Submedan Templat:Math adalah medan terkecil, karena menurut definisi medan memiliki setidaknya dua elemen berbeda Templat:Math.

Kolom hingga yang sederhana, dengan tatanan utama langsung diakses menggunakan aritmetika modular. Untuk bilangan bulat positif tetap Templat:Math, aritmetika "modulo Templat:Math" artinya melakukan dengan angka

Templat:Math

Penambahan dan perkalian pada himpunan ini dilakukan dengan melakukan operasi yang dimaksud himpunan bilangan bulat Templat:Math, membagi dengan Templat:Math dan mengambil sisanya sebagai hasil. Konstruksi ini menghasilkan bidang persis jika Templat:Math adalah bilangan prima. Misalnya mengambil bilangan prima Templat:Math hasil di bidang yang disebutkan di atas Templat:Math. Untuk Templat:Math dan secara lebih umum, untuk setiap bilangan komposit (yaitu, bilangan apa pun Templat:Math yang dapat diekspresikan sebagai produk Templat:Math dari dua bilangan asli yang lebih kecil), Templat:Math bukan bidang: produk dari dua elemen bukan nol adalah nol karena Templat:Math pada Templat:Math, yang, seperti yang dijelaskan di atas, dengan Templat:Math dari menjadi lapangan. Lapangan Templat:Math dengan Templat:Math elemen (Templat:Math menjadi prima) dibangun dengan cara ini biasanya dilambangkan dengan Templat:Math.

Setiap bidang terbatas yang dimiliki Templat:Math adalah Templat:Math elemen, di mana Templat:Math adalah bilangan prima dan Templat:Math. Pernyataan ini berlaku karena Templat:Math dapat dilihat sebagai ruang vektor di atas bidang utamanya. dimensi dari ruang vektor ini harus terbatas, katakanlah Templat:Math, yang menyiratkan pernyataan yang ditegaskan.^[7]

Bidang dengan Templat:Math elemen dapat dibuat sebagai bidang pemisah dari polinomial

Templat:Math.

Bidang pemisahan seperti itu merupakan perpanjangan dari Templat:Math di mana polinomial Templat:Math memiliki Templat:Math nol. Ini berarti Templat:Math memiliki angka nol sebanyak mungkin karena derajat dari Templat:Math adalah Templat:Math. Untuk Templat:Math, itu dapat diperiksa kasus per kasus menggunakan tabel perkalian di atas yang keempat elemennya Templat:Math memenuhi persamaan Templat:Math, jadi mereka adalah nol Templat:Math. Sebaliknya, pada Templat:Math, Templat:Math hanya memiliki dua angka nol (yaitu 0 dan 1), jadi Templat:Math tidak dibagi menjadi faktor linier dalam bidang yang lebih kecil ini. Menguraikan lebih lanjut pengertian teori medan dasar, dapat ditunjukkan bahwa dua bidang berhingga dengan urutan yang sama adalah isomorfik.^[8] Oleh karena itu, adalah kebiasaan untuk menyebut bidang berhingga dengan elemen Templat:Math, dilambangkan dengan Templat:Math atau Templat:Math.

Sejarah

Secara historis, tiga disiplin ilmu aljabar mengarah pada konsep bidang: soal menyelesaikan persamaan polinomial, teori bilangan aljabar, dan geometri aljabar.^[9] Langkah pertama menuju gagasan bidang dibuat pada tahun 1770 oleh Joseph-Louis Lagrange, yang mengamati bahwa mengubah angka nol Templat:Math dari polinomial kubik dalam pernyataan tersebut

Templat:Math

(dengan Templat:Math menjadi akar persatuan ketiga) hanya menghasilkan dua nilai. Dengan cara ini, Lagrange secara konseptual menjelaskan metode solusi klasik Scipione del Ferro dan François Viète, yang melanjutkan dengan mengurangi persamaan kubik untuk Templat:Math yang tidak diketahui menjadi persamaan kuadrat untuk Templat:Math.^[10] Bersama dengan pengamatan serupa untuk persamaan derajat 4, Lagrange menghubungkan apa yang akhirnya menjadi konsep bidang dan konsep grup.^[11] Vandermonde, juga pada tahun 1770, dan secara lebih luas, Carl Friedrich Gauss, dalam karyanya Disquisitiones Arithmeticae (1801), mempelajari persamaan

Templat:Math

untuk bilangan prima Templat:Math dan, lagi-lagi menggunakan bahasa modern, hasil siklik grup Galois. Gauss menyimpulkan bahwa [[poligon beraturan|regular Templat:Math-gon]] dapat dibangun jika Templat:Math. Berdasarkan karya Lagrange, Paolo Ruffini menyatakan (1799) bahwa persamaan kuintik s (persamaan polinomial derajat 5) tidak dapat diselesaikan secara aljabar; Namun, argumennya salah. Celah ini diisi oleh Niels Henrik Abel pada tahun 1824.^[12] Évariste Galois, pada tahun 1832, merancang kriteria yang diperlukan dan cukup agar persamaan polinomial dapat dipecahkan secara aljabar, sehingga menetapkan efek yang sekarang dikenal sebagai teori Galois. Baik Abel dan Galois bekerja dengan apa yang sekarang disebut bidang angka aljabar, tetapi tidak memahami gagasan eksplisit tentang bidang, atau pun grup.

Pada tahun 1871 Richard Dedekind diperkenalkan, untuk satu set bilangan real atau kompleks yang ditutup di bawah empat operasi aritmatika, kata Jerman Körper , yang berarti "tubuh" atau "korpus" (untuk menyarankan entitas yang tertutup secara organik). Istilah Inggris "field" diperkenalkan oleh Templat:Harvtxt.^[13]

Templat:Quote

Pada tahun 1881 Leopold Kronecker mendefinisikan apa yang dia sebut sebagai domain rasionalitas , yang merupakan bidang pecahan rasional dalam istilah modern. Gagasan Kronecker tidak mencakup bidang semua bilangan aljabar (yang merupakan bidang dalam pengertian Dedekind), tetapi di sisi lain lebih abstrak daripada Dedekind karena tidak membuat asumsi khusus tentang sifat elemen suatu bidang. Kronecker menafsirkan bidang seperti Templat:Math secara abstrak sebagai bidang fungsi rasional Templat:Math. Sebelum ini, contoh bilangan transendental telah diketahui sejak karya Joseph Liouville pada tahun 1844, sampai Charles Hermite (1873) dan Ferdinand von Lindemann (1882) membuktikan transendensi Templat:Math dan Templat:Math.^[14]

Medan dengan struktur tambahan

Sejak medan ada di mana-mana dalam matematika dan seterusnya, beberapa penyempurnaan konsep telah disesuaikan dengan kebutuhan bidang matematika tertentu.

Medan tatanan

Templat:Main Medan F disebut medan tatanan jika terdapat dua elemen yang dapat dibandingkan, sehingga Templat:Math dan Templat:Math dengan Templat:Math dan Templat:Math. Misalnya, bilangan riil membentuk Medan tatanan, dengan tatanan seperti biasa Templat:Math. Teorema Artin–Schreier menyatakan bahwa suatu medan diurutkan jika dan hanya jika itu adalah medan riil secara formal, yang berarti bahwa persamaan kuadrat apa pun

x_{1}^{2} + x_{2}^{2} + \dots + x_{n}^{2} = 0

hanya solusi Templat:Math.^[15] Himpunan semua kemungkinan tatanan pada medan tetap Templat:Math isomorfik ke himpunan gelanggang homomorfisme dari gelanggang Witt Templat:Math dari bentuk kuadrat berakhir dengan Templat:Math, sebagai Templat:Math.^[16]

Sebuah medan Archimedean adalah medan yang diurutkan sedemikian rupa sehingga untuk setiap elemen terdapat ekspresi hingga

Templat:Math

yang nilainya lebih besar dari elemen itu, artinya tidak ada elemen tak hingga. Sama halnya, medan yang tidak digunakan infinitesimal (elemen lebih kecil dari semua bilangan rasional); atau, ekuivalen medan isomorfik ke submedan dari Templat:Math.

Bidang yang diurutkan adalah Dedekind-complete jika semua batas atas, batas bawah (lihat kelengkapan Dedekind) dan batas. Secara lebih formal, setiap himpunan bagian hingga dari Templat:Math harus memiliki batas atas terkecil. Setiap medan lengkap tetap menggunakan Archimedean,^[17] karena dalam medan non-Archimedean tidak terdapat rasional yang sangat kecil atau paling tidak positif, darimana tatanannya Templat:Math, setiap elemen yang lebih besar dari kecil, tidak memiliki batas.

Karena setiap subkolom riil menggunakan celah seperti itu, Templat:Math adalah kolom tatanan lengkap unik, hingga isomorfisme.^[18] Beberapa hasil dasar dalam kalkulus mengikuti langsung dari karakterisasi riil ini.

Hiperriil Templat:Math membentuk Medan tatanan yang bukan Archimedean. Ini adalah ekstensi dari riil yang diperoleh dengan memasukkan bilangan tak hingga dan infinitesimal tak hingga. Ini lebih besar masing-masing lebih kecil dari bilangan riil. Hiperriil membentuk dasar dasar analisis non-standar.

Medan topologi

Perbaikan lain dari pengertian bidang adalah medan topologi, dimana himpunan Templat:Math adalah ruang topologi, maka semua operasi medan (penambahan, perkalian, peta Templat:Math dan Templat:Math) adalah peta kontinu sehubungan dengan topologi ruang.^[19] Topologi semua medan yang dibahas di bawah ini diinduksi dari metrik, yaitu fungsi

Templat:Math

yang mengukur jarak antara dua elemen Templat:Math.

Pelengkapan dari Templat:Math adalah medan lain dimana "celah" di medan asli Templat:Math. Misalnya, bilangan irasional Templat:Math, misal Templat:Math, adalah "celah" dalam rasio Templat:Math dalam arti bahwa ini adalah bilangan riil yang didekati secara acak oleh bilangan rasional Templat:Math, dalam arti jarak Templat:Math dan Templat:Math diberikan nilai mutlak Templat:Math. Tabel berikut mencantumkan beberapa contoh konstruksi ini. Kolom keempat menunjukkan contoh nol urutan, yaitu, urutan yang batasnya (untuk Templat:Math) adalah nol.

Medan	Metrik	Pelengkapan	Tatanan nol
Templat:Math	Templat:Math (biasa nilai absolut)	R	Templat:Math
Templat:Math	diperoleh dengan menggunakan valuasi p-adik, untuk bilangan prima Templat:Math	Templat:Math ([[bilangan p-adik\|bilangan Templat:Math-adic]])	Templat:Math
Templat:Math (Templat:Math bidang apapun)	diperoleh dengan menggunakan valuasi Templat:Math-adik	Templat:Math	Templat:Math

Medan diferensial

Medan diferensial adalah medan yang dilengkapi dengan turunan, yaitu, memungkinkan untuk mengambil turunan elemen di medan.^[20] Misalnya, medan R(X), dengan turunan standar polinomial membentuk medan diferensial. Medan ini adalah pusat teori Galois diferensial, varian dari teori Galois yang berhubungan dengan persamaan diferensial linear.

Gagasan terkait

Selain struktur tambahan dengan menggunakan medan, medan menerima berbagai gagasan terkait lainnya. Karena dalam medan 0 ≠ 1, medan memiliki setidaknya dua elemen. Meskipun demikian, ada konsep medan dengan satu elemen yang disarankan untuk menjadi batas medan hingga Templat:Math, karena Templat:Math cenderung 1.^[21] Selain gelanggang pembagian, ada berbagai yang lebih lemah lainnya, struktur aljabar yang terkait dengan medan seperti medan kuasi, medan dekat dan medan semimedan.

Ada juga kelas kesesuai dengan struktur medan, yang terkadang disebut Medan (atau Field), dengan huruf besar M. Bilangan surriil membentuk medan riil, dan akan menjadi medan kecuali fakta bahwa mereka adalah kelas yang tepat, bukan satu himpunan. Angka adalah konsep dari teori permainan, untuk medan seperti itu juga.^[22]

Gelanggang pembagian

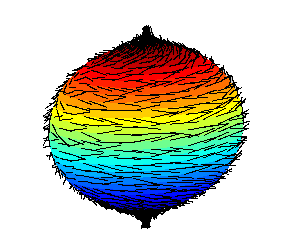
Teorema bola berbulu menyatakan bahwa bola tidak bisa disisir. Secara formal, tidak ada kontinu medan vektor singgung pada bola Templat:Math, yang di mana-mana bukan nol.

Menjatuhkan satu atau beberapa aksioma dalam definisi medan mengarah ke struktur aljabar lainnya. Seperti disebutkan di atas, gelanggang komutatif memenuhi semua aksioma medan, kecuali untuk invers perkalian. Menjatuhkan kondisi bahwa perkalian bersifat komutatif mengarah ke konsep gelanggang pembagian atau medan miring.^{[nb 2]} Gelanggang pembagian satu-satunya yang berdimensi-hingga vektor-Templat:Math ruang Templat:Math sendiri, Templat:Math (yang merupakan medan), kuaternion Templat:Math (dimana perkalian tidak komutatif), dan oktonion Templat:Math (dimana perkalian tidak bersifat komutatif atau asosiatif). Fakta ini dibuktikan dengan menggunakan metode topologi aljabar pada tahun 1958 oleh Michel Kervaire, Raoul Bott, dan John Milnor.^[23] Tidak adanya aljabar pembagian berdimensi ganjil lebih klasik. Ini dapat disimpulkan dari teorema bola berbulu yang diilustrasikan di sebelah kanan.Templat:Citation needed

Catatan

Templat:Reflist

Referensi

Templat:Wikibooks

Templat:Refbegin

Templat:Citation
Templat:Citation
Templat:Citation, especially Chapter 13
Templat:Citation
Templat:Citation
Templat:Citation
Templat:Citation
Templat:Citation
Templat:Citation. See especially Book 3 (Templat:ISBN) and Book 6 (Templat:ISBN).
Templat:Citation
Templat:Citation
Templat:Citation
Templat:Citation
Templat:Citation
Templat:Citation
Templat:Citation
Templat:Citation
Templat:Citation
Templat:Citation
Templat:Citation
Templat:Citation
Templat:Citation
Templat:Citation
Templat:Springer
Templat:Citation
Templat:Citation
Templat:Citation
Templat:Citation
Templat:Citation
Templat:Citation
Templat:Citation
Templat:Citation
Templat:Citation
Templat:Citation
Templat:Citation
Templat:Citation
Templat:Citation
Templat:Citation
Templat:Citation
Templat:Citation
Templat:Citation
Templat:Citation
Templat:Citation
Templat:Citation
Templat:Citation
Templat:Citation
Templat:Citation
Templat:Citation
Templat:Citation
Templat:Citation
Templat:Citation
Templat:Citation
Templat:Citation
Templat:Citation

Templat:Refend

Kesalahan pengutipan: Ditemukan tag <ref> untuk kelompok bernama "catatan", tapi tidak ditemukan tag <references group="catatan"/> yang berkaitan
Kesalahan pengutipan: Ditemukan tag <ref> untuk kelompok bernama "nb", tapi tidak ditemukan tag <references group="nb"/> yang berkaitan

[Beachy_2006_loc=p._120,_Ch._3-1] 1,0 ^1,1 Templat:Harvtxt

[2] Templat:Harvtxt

[3] Templat:Harvtxt

[6] Templat:Harvtxt

[7] Templat:Harvtxt

[9] Templat:Harvtxt

[10] Templat:Harvtxt

[11] Templat:Harvtxt

[12] Templat:Harvtxt

[13] Templat:Harvtxt

[14] Templat:Harvtxt

[15] Templat:Harvtxt

[16] Penggunaan Paling Awal dari Beberapa Kata Matematika (F)

[17] Templat:Harvtxt

[18] Templat:Harvtxt

[19] Templat:Harvtxt

[20] Templat:Harvtxt

[21] Templat:Harvtxt

[22] Templat:Harvtxt

[23] Templat:Harvtxt

[24] Templat:Harvtxt

[25] Templat:Harvtxt

[27] Templat:Harvtxt

[1]

[2]

[3]

[catatan 1]

[nb 1]

[4]

[5]

[catatan 2]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[nb 2]

[23]

Lapangan (matematika)

Daftar isi

Definisi