Deret harmonik (matematika)

Dalam matematika, deret harmonik adalah deret takhingga divergen

$\sum _{n=1}^{\mathrm{\infty }}\frac{1}{n}=1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\frac{1}{5}+\cdots .$

Namanya diturunkan dari konsep nada tambahan, atau harmonik dalam musikː panjang gelombangnya dari nada tambahan dari sebuah dawai yang bergetar adalah $\frac{1}{2}$, $\frac{1}{3}$, $\frac{1}{4}$, dst., dari panjang gelombang dasar dawai. Setiap suku dari deretnya setelah pertamanya adalah purata harmonik dari suku-suku tetangga, frasa purata harmonik juga diturunkan dari musik.

Sejarah

Divergensi dari deret harmonik pertama kali dibuktikan dalam abad ke-14 oleh Nicole Oresme, tetapi prestasi ini jatuh dalam ketidakjelasan. Bukti-bukti diberikan dalam abad ke-17 oleh Pietro Mengoli dan oleh Johann Bernoulli, bukti terakhir dipublikasikan dan dipopulerkan oleh saudara laki-lakinya Jacob Bernoulli.

Menurut sejarah, barisan harmonik memiliki popularitas tertentu dengan arsitek-arsitek. Ini sangat khusus dalam periode Barok, ketika arsitek-arsitek menggunakan mereka untuk medirikan proporsi denah lantai, ketinggian, dan untuk membangun hubungan harmonik antara detail arsitektur interior dan eksterior gereja dan istana.

Divergensi

Terdapat beberapa bukti-bukti terkenal dari kedivergenan dari deret harmonik. Beberapa dari mereka diberikan di bawah.

Uji perbandingan

Salah satu cara untuk membuktikan kedivergenan adalah membandingkan deret harmonik dengan deret divrergen, dimana setiap penyebut digantikan dengan pangkat dari dua terbesar berikutnyaː

$\begin{array}{cccccccccccccccccc}1& +\frac{1}{2}& & +\frac{1}{3}& & +\frac{1}{4}& & +\frac{1}{5}& & +\frac{1}{6}& & +\frac{1}{7}& & +\frac{1}{8}& & +\frac{1}{9}& & +\cdots \\ \ge 1& +\frac{1}{2}& & +\frac{1}{\mathrm{𝟒}}& & +\frac{1}{4}& & +\frac{1}{\mathrm{𝟖}}& & +\frac{1}{\mathrm{𝟖}}& & +\frac{1}{\mathrm{𝟖}}& & +\frac{1}{8}& & +\frac{1}{\mathrm{𝟏}\mathrm{𝟔}}& & +\cdots \end{array}$

Setiap suku darai deret harmonik lebih besar atau sama dengan suku yang sesuai dari deret kedua, dan oleh karena itu jumlah dari deret harmonik harus lebih besar dariada sama dengan jumlah dari deret kedua. Namun, jumlah dari deret kedua adalah takhinggaː

$\begin{array}{cc}& 1+\left(\frac{1}{2}\right)+(\frac{1}{4}+\frac{1}{4})+(\frac{1}{8}+\frac{1}{8}+\frac{1}{8}+\frac{1}{8})+(\frac{1}{16}+\cdots +\frac{1}{16})+\cdots \\ =& 1+\frac{1}{2}+\frac{1}{2}+\frac{1}{2}+\frac{1}{2}+\cdots =\mathrm{\infty }.\end{array}$

Itu diikuti (oleh uji perbandingan) bahwa jumlah dari deret harmonik harus takhingga juga. Lebih tepatnya, perbandingan di atas membuktikan bahwa

$\sum _{n=1}^{2^k}\frac{1}{n}\ge 1+\frac{k}{2}$

untuk setiap bilangan bulat positif $k$.

Bukti ini, diusulkan oleh Nikol Oresme pada tahun 1350, dianggap oleh banyak orang di komunitas matematikaTemplat:By whom menjadi titik tertinggi di matematika abad pertengahan. Ini masih menjadi bukti standar yang diajarkan di kelas matematika saat ini. Uji kondensansi Cauchy adalah sebuah generalisasi dari argumen ini.

Uji integral

Ilustrasi dari uji integral.

Ini memungkinkan untuk membuktikan bahwa deret harmonik divetgen dengan membandingkan jumlahnya dengan sebuah integral takwajar. Secara khusu, tinjau susunan persegi panjang-persegi panjang yang diberikan dalam gambar di sebelah kanan. Setiap persegi panjang adalah 1 satuan lebar dan $\frac{1}{n}$ satuan panjang, jadi luas total dari jumlah takhingga persegi panjang adalah jumlah dari deret harmonik.

$\begin{array}{c}\text{luas}\\ \text{persegi panjang}\end{array}=1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\frac{1}{5}+\cdots$Sebagai tambahan, luas total di bawah kurva $y=\frac{1}{x}$ dari $1$ ke takhingga diberikan oleh sebuah integral takwajar divergen.ː

$\begin{array}{c}\text{luas dibawah}\\ \text{kurva}\end{array}=\underset{1}{\overset{\mathrm{\infty }}{\int }}\frac{1}{x}dx=\mathrm{\infty }.$

Karena luas ini menyeluruh terkandung dalam persegi panjang, luas total dari persegi panjang harus takhingga juga. Lebih tepatnya, ini membuktikan bahwa

$\sum _{n=1}^k\frac{1}{n}>\underset{1}{\overset{k+1}{\int }}\frac{1}{x}dx=\ln (k+1).$

Generalisasi argumen ini dikenal sebagai uji integral.

Rerata kedivergensi

Deret harmonik divergen secara perlahan. Sebagai contoh, jumlah dari suku $10^{43}$ pertama kurang dari $100$. Ini dikarenakan jumlah parsial dari deretnya memiliki pertumbuhan logaritmik. Khususnya,

$\sum _{n=1}^k\frac{1}{n}=\ln k+\gamma +{\epsilon }_k\le (\ln k)+1$

dimana $\gamma$ adalah konstanta Euler–Mascheroni dan ${\epsilon }_k\sim \frac{1}{2k}$ yang mendekati karena $k$ menuju takhingga Leonhard Euler membuktikan baik ini dan juga fakta yang lebih mencolok bahwa jumlah yang mencakup kebalikan bilangan prima juga divergen, yaitu

$\sum _{p\text{ bilangan prima }}\frac{1}{p}=\frac{1}{2}+\frac{1}{3}+\frac{1}{5}+\frac{1}{7}+\frac{1}{11}+\frac{1}{13}+\frac{1}{17}+\cdots =\mathrm{\infty }.$

Jumlah parsial

Templat:Small

Templat:Mvar	Jumlah parsial dari deret harmonik, Templat:Mvar
	diekspresikan sebagai sebuah pecahan		desimal	ukuran relatif
1	1		Templat:0Templat:Bartable
2	3	/2	Templat:0Templat:Bartable
3	11	/6	~Templat:Bartable
4	25	/12	~Templat:Bartable
5	137	/60	~Templat:Bartable
6	49	/20	Templat:0Templat:Bartable
7	363	/140	~Templat:Bartable
8	761	/280	~Templat:Bartable
9	Templat:Val	/Templat:Val	~Templat:Bartable
10	Templat:Val	/Templat:Val	~Templat:Bartable
11	Templat:Val	/Templat:Val	~Templat:Bartable
12	Templat:Val	/Templat:Val	~Templat:Bartable
13	Templat:Val	/Templat:Val	~Templat:Bartable
14	Templat:Val	/Templat:Val	~Templat:Bartable
15	Templat:Val	/Templat:Val	~Templat:Bartable
16	Templat:Val	/Templat:Val	~Templat:Bartable
17	Templat:Val	/Templat:Val	~Templat:Bartable
18	Templat:Val	/Templat:Val	~Templat:Bartable
19	Templat:Val	/Templat:Val	~Templat:Bartable
20	Templat:Val	/Templat:Val	~Templat:Bartable
21	Templat:Val	/Templat:Val	~Templat:Bartable
22	Templat:Val	/Templat:Val	~Templat:Bartable
23	Templat:Val	/Templat:Val	~Templat:Bartable
24	Templat:Val	/Templat:Val	~Templat:Bartable
25	Templat:Val	/Templat:Val	~Templat:Bartable
26	Templat:Val	/Templat:Val	~Templat:Bartable
27	Templat:Val	/Templat:Val	~Templat:Bartable
28	Templat:Val	/Templat:Val	~Templat:Bartable
29	Templat:Val	/Templat:Val	~Templat:Bartable
30	Templat:Val	/Templat:Val	~Templat:Bartable

Jumlah-jumlah parsial terhingga dari deret harmonik divergen,

$H_n=\sum _{k=1}^n\frac{1}{k},$

disebut bilangan harmonik

Selisih antara $H_n$ dan $\ln n$ konvergen dengan konstanta Euler–Mascheroni. Selisih antara setiap dua bilangan harmonik tidak pernah sebuah bilangan bulat. Tidak ada bilangan harmonik adalah bilangan bulat, kecuali untuk $H_1=1$.Templat:RpTemplat:Rp

Deret yang berkaitan

Deret harmonik bolak-balik

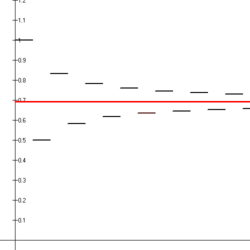
Jumlah parsial empat belas pertama dari deret harmonik bergantian (segmen garis berwarna hitam) menunjukkan kekonvergenan pada logaritma natural 2 (garis berwarna merah).

Deret

$\sum _{n=1}^{\mathrm{\infty }}\frac{(-1{)}^{n+1}}{n}=1-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}+\frac{1}{5}-\cdots$

dikenal sebagai deret harmonik bolak-balik. Deret ini konvergen oleh uji deret bolak-balik. Khususnya, jumlahnya sama dengan logaritma natural 2ː

$1-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}+\frac{1}{5}-\cdots =\ln 2.$

Deret harmonik bolak-balik, sementara konvergen bersyarat, tidak sepenuhnya konvergen: jika asuku-suku dalam deret diatur ulang secara sistematis, secara umum jumlahnya menjadi berbeda dan , bergantung pada penyusunan kembali, bahkan mungkin takhingga.

Rumus deret harmonik bolak-balik adalah sebuah kasus spesial dari deret Mercator, deret Taylor untuk logaritma natural.

Sebuah deret berkaitan bisa diturunkan dari deret Taylor untuk arctangenː

$\sum _{n=0}^{\mathrm{\infty }}\frac{(-1{)}^n}{2n+1}=1-\frac{1}{3}+\frac{1}{5}-\frac{1}{7}+\cdots =\frac{\pi }{4}.$

Iini dikenal sebagai deret Leibniz.

Deret harmonik umum

Deret harmonik umum adalah dari bentuk

$\sum _{n=0}^{\mathrm{\infty }}\frac{1}{an+b},$

dimana $a\ne 0$ dan $b$ adalah bilangna real, dan $\frac{b}{a}$ bukan nol atau sebuah bilangan bulat negatif.

Dengan uji perbandingan limit dengan deret harmonik, semua deret harmonik umum juga divergen.

Deret-p

Sebuah generalisasi dari deret harmonik adalah deret-p (atau deret hiperharmonik), didefinisikan sebagai

$\sum _{n=1}^{\mathrm{\infty }}\frac{1}{n^p}$

untuk setiap bilangan real $p$. Ketika $p=1$, deret-p adalah deret harmonik, yang divergen. Baik itu uji integral atau uji kondensasi Cauchy menunjukkan bahwa deret-p konvergen untuk semua $p>1$ (dalam hal ini disebut deret lebih-harmonik) dan divergen untuk semua $p\le 1$. Jika $p>1$ maka jumlah dari deret-p adalah $\zeta (p)$, yaitu fungsi zeta Riemann dievaluasi sebagai $p$

Masalah mencari jumlah untuk $p=2$ disebut masalah Basel; Leonhard Euler menunjukkan ini bernilai $\frac{{\pi }^2}{6}$. Nilai dari jumlah untuk $p=3$ disebut konstanta Apéry, karena Roger Apéry membuktikan bahwa itu adalah sebuah bilangan irasional.

Deret-ln

Berkaitan dengan deret-p adalah deret-ln, didefinisikan sebagai

$\sum _{n=2}^{\mathrm{\infty }}\frac{1}{n(\ln n{)}^p}$

untuk setiap bilangan real positif $p$. Ini bisa ditunjukkan oleh uji integral untuk divergen untuk $p\le 1$ tetapi onvergen untuk semua $p>1$.

Deret-φ

Untuk setiap cembung, fungsi bernilai real $\phi$ seperti

$\underset{u\to 0^{+}}{\mathrm{lim\; sup}}\frac{\phi \left(\frac{u}{2}\right)}{\phi (u)}<\frac{1}{2},$

deret

$\sum _{n=1}^{\mathrm{\infty }}\phi \left(\frac{1}{n}\right)$

konvergen.Templat:Citation needed

Deret harmonik acak

Deret harmonik acak

$\sum _{n=1}^{\mathrm{\infty }}\frac{s_n}{n},$

dimana $s_n$ adalah independen, variabel acak terdistribusi identik yang mengambil nilai $+1$ dan $-1$ dengan propabilitas sama dengan $\frac{1}{2}$, dikenal sebagai sebuah contoh dalam teori probabilitas dengan probabilitas 1. Fakta kekonvergenan ini adalah konsekuensi mudah dari teorema tiga deret Kolmogorov atau dari pertidaksamaan maksimal Kolmogorov yang terkait erat. Borin Schmuland dari Universitas Alberta lebih lanjut memeriksa sifat-sifat dari deret harmonik acak, dan menunjukkan bahwa deret konvergen adalah sebuah variabel acak dengan beberapa sifat-sifat yang menarik. Khususnya, fungsi kepekatan probabilitas dari variabel acak ini dievalusi pada $+2$ atau pada $-2$ mengambil nilai $0.124999999999999999999999999999999999999999764\dots$, berbeda dari $\frac{1}{8}$ kurang dari $10^{-42}$. Makalah Schmuland menjelaskan mengapa probabilitas ini sangat dekat, tetapi tidak persis, $\frac{1}{8}$. Nilai pasti dari probabilias ini diberikan oleh integral produk kosinus takhingga $C_2$ dibagi oleh $\pi$.

Deret harmonik habis

Deret harmonik habis dimana semua dari suku-suku yang digit 9 muncul dimana saja dalampenyebut dihapus dapat ditampilkan untuk konvergen ke nilai $22.92067661926415034816\dots$.. Faktanya, ketika semua suku berisi setiap deretan bilangan tertentu (dalam setiap basis) dihilangkan, deretnya konvergen.

Penerapan

Deret harmonik bisa berlawanan dengan intuisi siswa yang pertama kali menjumpainya, itu adalah sebuah deret divergen meskipun limit dari suku ke-$n$ saat $n$ menuju ke takhingga adalah nol. Kedivergenan dari deret harmonik juga merupakan sumber dari beberapa paradoks yang jelas. Salah satu dari contoh-contoh ini adalah "cacing di gelang karet". Andaikan bahwa sebuah cacing merangkak di sekitar karet gelang satu meter dengan elastis takhingga pada saat yang sama saat karet gelang direngangkan terdistribusi secara merata. Jika cacing berjalan 1 cm per meint dan karetnya meregang 1 meter per menit, akankah cacing mencapai akhir dari gelang karet? Jawabannya. secara berlawanan, "ya", untuk setelah $n$ menit, rasionya dari jarak berpergian oleh cacing dengan panjang totoal dari gelang karet adalah

$\frac{1}{100}\sum _{k=1}^n\frac{1}{k}.$

(Faktanya rasio sebenarnya sedikit kurang dari penjumlahan ini karena gelang memanjang terus-menerus.)

Karena deeretnya menjadi besar secara sebarang saat $n$ menjadi besar, akhirnya rasio ini harus melebihi 1, yang menyiratkan bahwa cacing mencapai akhir dari gelang karet. Namun, nilai $n$ di mana ini terjadi harus sangat besar; sekitar $e^{100}$, sebuah bilangan melebihi $10^{43}$ menit ($10^{37}$ tahun). Meskipun deret harmonik divergen, itu melakukannya dengan sangat lambat.

Masalah lainnya melibatkan deret harmonik adalah masalah jip, yang (dalam satu bentuk) menanyakan berapa total bahan bakar yang dibutuhkan untuk sebuah jip dengan daya dukung bahan bakar yang terbatas untuk menyeberangi gurun, kemungkinan menyebabkan penurunan bahan bakar di sepanjang rute. Jarak yang bisa dilintasi dengan jumlah bahan bakar berkaitan dengan jumlah parsial dari deret harmonik, yang tumbuh secara logaritmik. Dan juga bahan bakar dibutuhkan meningkat secara eksponensial dengan jarak yang diinginkan.

Masalah penumpukan balok, balok-balok sejajar menurut jembatan pembelahan deret harmonik dari setiap lebar.

Contoh lain adalah masalah penumpukan balok, diberikan sebuah kumpulan domino yang identik, ini jelas mungkin untuk menumpukkan mereka pada tepi dari sebuah meja sehingga mereka menggantung di tepi dari meja tanpa jatuh. Hasil yang berlawanan dengan intuisi adalah bahwa salah satu bisa menumpukkan mereka sedemikian rupa untuk membuat bergantungan menjadi besar, asalkan ada domnio yang cukup.

Sebuah contoh yang lebih sederhana, di samping itu, adalah perenang yang tetap menambahkan lebih banyak kecepatan ketika menyentuh tembok dari kolam. Perenang mulai melintasi sebuah kolam 10 meter pada sebuah kecepatan 2 m.s, dan dengan setiap lintasan, 2 m/s lainnya ditambahkan ke kecepatan. Dalam teori, kecepatan perenang adalah tak terbatas, tetapi jumlah lintasan yang dibutuhkan untuk mencapai kecepatan itu menjadi sangat besar; contohnya, untuk mencapai kecepatan cahaya (abaikan relativitas khusus), perenang membutuhkan untuk melintasi kolam 150 juta kali. Berbeda dengan jumlah besar ini, waktu yang dibutuhkan untuk mencapai sebuah keceptan yang diberikan tergantung pada penjumlahan dari deretnya pada setiap diberikan jumlah lintasan kolam (berulang)ː

$\frac{10}{2}\sum _{k=1}^n\frac{1}{k}.$

Menghitung jumlah (secara berulang) menunjukkan bahwa untuk mencapai kecepatan cahaya, waktu yang dibutuhkan hanya 97 detik. Dengan melanjtukan melampaui titik ini (melebihi kecepatan cahaya, lagi abaikan relativitas khusus), waktu yang diambil untuk melintasi kolam pada kenyataannya akan mendekati nol saat jumlah berulang menjadi sangat besar, da meskipun waktu yang dibutuhkan untuk melintasi kolam muncul untuk cenderung ke nol (pada sebuah bilangan takhingga berulang), jumlah berulang (waktu yang diberikan untuk total lintasan kolam) akan tetap divergen pada sebuah divergen dengan kecepatan yang sangat lambat.

Lihat pula

• Barisan harmonik
• Daftar jumlah timbal balik
• Fungsi eta Dirichlet

Pranala luar

• Templat:SpringerEOM
• Templat:Cite journal
• Templat:MathWorld
• Templat:MathWorld
• Templat:Cite journal