Sinus dan kosinus

Dalam matematika, sinus dan kosinus adalah fungsi trigonometri untuk sudut. Sinus dan kosinus dari suatu sudut lancip didefinisikan dalam konteks segitiga siku-siku: nilai sinus adalah rasio dari panjang sisi segitiga yang menghadap sudut tersebut (sisi tegak) terhadap panjang sisi terpanjang segitiga (hipotenusa), sedangkan nilai kosinus adalah rasio panjang sisi segitiga yang lain (sisi alas) terhadap hipotenusa. Untuk suatu sudut $x$, fungsi sinus dan kosinus dituliskan sebagai $\sin x$ and $\cos x$.

Lebih umum lagi, definisi sinus dan kosinus dapat diperluas ke sembarang nilai real, dalam konteks panjang suatu segmen garis pada suatu lingkaran satuan. Definisi yang lebih modern menyatakan sinus dan kosinus dalam bentuk deret tak hingga, atau solusi dari suatu persamaan diferensial, yang memungkinkan memperluasnya ke bilangan negatif dan bahkan ke bilangan kompleks.

Fungsi sinus dan kosinus umum digunakan untuk memodelkan fenomena periodik seperti bunyi dan gelombang suara, posisi dan kecepatan dari osilator harmonik, intensitas cahay matahari dan panjang hari, maupun variasi temperatur sepanjang tahun.

Fungsi sinus dan kosinus dapat dilacak kembali ke fungsi jyā dan koṭi-jyā yang digunakan pada astronomi India pada periode Gupta (Aryabhatiya, Surya Siddhanta), yang mengalami penerjemahan dari bahasa Sanskerta ke bahasa Arab, kemudian dari bahasa Arab ke bahasa Latin. Kata "sinus" berasal dari penerjemahan bahasa Latin yang salah oleh Robert of Chester untuk kata Arab jiba, yang selanjutnya merupakan transliterasi dari kata Sanskerta untuk setengah busur, jya-ardha. Kata "cosinus" (Indonesia: "kosinus") berasal dari singkatan Latin "complementi sinus" pada abad pertengahan.

Definisi dengan segitiga siku-siku

Untuk suatu sudut α, fungsi sinus memberikan rasio panjang sisi tegak dengan panjang hipotenusa

Untuk mendefinisikan sinus dan kosinus dari suatu sudut lancip α, mulai dengan membentuk segitiga siku-siku yang mengandung sudut α; pada gambar berikut, sudut α pada segitiga ABC adalah sudut yang ingin dihitung. Ketiga sisi pada segitiga diberi nama sebagai berikut:

• Sisi tegak atau sisi berlawanan adalah sisi yang menghadap sudut α; dalam kasus ini adalah sisi a.
• Hipotenusa adalah sisi yang menghadap sudut siku-siku, dalam kasus ini adalah sisi h. Hipotenusa selalu merupakan sisi terpanjang dari sembarang segitiga siku-siku.
• Sisi samping adalah sisi segitiga yang tersisa, dalam kasus ini adalah sisi b. Sisi ini diapit oleh sudut α dan sudut siku-siku.

Setelah segitiga tersebut dibentuk, sinus dari sudut adalah panjang dari sisi tegak dibagi dengan panjang hipotenusa:

$\sin (\alpha )=\frac{\text{sisi tegak}}{\text{hipotenusa}}\cos (\alpha )=\frac{\text{sisi alas}}{\text{hipotenusa}}$

Fungsi-fungsi trigometri yang lain dapat didefinisikan dengan cara yang mirip; sebagai contoh, tangen dari suatu sudut adalah rasio antara sisi tegak dengan sisi alas.

Dari definisi, nilai dari $\sin (\alpha )$ dan $\cos (\alpha )$ terlihat bergantung pada pemilihan segitiga siku-siku yang mengandung sudut α. Namun, hal ini tidak benar, karena semua segitiga siku-siku yang mengandung sudut α akan serupa, sehingga rasio yang didapatkan dari semua segitiga tersebut akan sama.

Definisi dengan lingkaran satuan

Animasi yang menunjukkan fungsi sinus (warna merah) digambarkan dari koordinat-y suatu titik pada lingkaran satuan (warna hijau), pada suatu sudut θ. Sedangkan, koordinat-x dari titik tersebut menghasilkan grafik kosinus (warna biru).

Dalam trigonometri, lingkaran satuan adalah lingkaran dengan jari-jari sebesar 1 dan berpusat di titik asal (0, 0) pada sistem koordinat Kartesius. Misalkan suatu segmen garis melalui titik asal, membentuk sudut

θ terhadap sisi positif dari sumbu-x, dan memotong lingkaran satuan pada suatu titik. Nilai koordinat-x dan -y dari titik tersebut sama dengan Templat:Math dan Templat:Math, secara berurutan.

Definisi ini konsisten dengan definisi dengan menggunakan segitiga siku-siku ketika 0 < θ < π/2. Karena panjang hipotenusa segitiga siku-siku di lingkaran satuan selalu bernilai 1, $\sin (\theta )=\frac{\text{sisi}\text{tegak}}{\text{hipotenusa}}=\frac{\text{sisi}\text{tegak}}{1}=\text{sisi}\text{tegak}$. Lebih lanjut, panjang sisi tegak dari segitiga ini adalah koordinat-y dari titik. Argumen yang sama dapat dibuat untuk menunjukkan $\cos (\theta )=\frac{\text{sisi alas}}{\text{hipotenusa}}$ ketika 0 < θ < π/2, bahkan ketika menggunakan definisi dengan lingkaran satuan. nilai tangen Templat:Math didefinisikan sebagai $\frac{\sin (\theta )}{\cos (\theta )}$, atau secara ekuivalen, sebagai kemiringan dari segmen garis.

Definisi menggunakan lingkaran satuan memiliki keuntungan bahwa nilai sudut dapat diperluas menjadi sembarang bilangan real. Hal ini juga dapat dicapai dengan menggunakan beberapa simetri, dan mengganggap sinus (dan kosinus) sebagai fungsi periodik.

Identitas

Fungsi sinus dan kosinus terhubung secara tepat (exact) oleh identitas berikut, yang berlaku untuk sembarang nilai $\theta$ (dalam radian):

$\sin (\theta )=\cos (\frac{\pi }{2}-\theta )=\cos (\theta -\frac{\pi }{2})$

$\cos (\theta )=\sin (\frac{\pi }{2}-\theta )=\sin (\theta +\frac{\pi }{2})$

Lawan perkalian

Invers perkalian dari sinus adalah kosekan, yang ditulis sebagai Templat:Math, atau Templat:Math. Kosekan memberikan rasio panjang hipotenusa terhadap panjang sisi tegak. Serupa dengan itu, invers perkalian dari kosinus adalah sekan, yang memberikan rasio panjang hipotenusa terhadap panjang sisi samping.

$\csc (A)=\frac{1}{\sin (A)}=\frac{\text{hipotenusa}}{\text{sisi tegak}}$

$\sec (A)=\frac{1}{\cos (A)}=\frac{\text{hipotenusa}}{\text{sisi alas}}$

Fungsi invers

The usual principal values of the Templat:Math and Templat:Math functions graphed on the Cartesian plane

Fungsi invers dari sinus adalah arcsinus (ditulis sebagai arcsin atau asin), atau invers sinus (Templat:Math). Fungsi invers dari kosinus adalah arccosinus, yang ditulis sebagai arccos, acos, atau Templat:Math. (simbol -1 pada bentuk Templat:Math dan Templat:Math melambangkan invers dari suatu fungsi, bukan perpangkatan.) Karena sinus dan kosinus bukan fungsi injektif, invers mereka hanya fungsi invers secara parsial. Sebagai contoh, Templat:Math, tapi begitu pula dengan Templat:Math, Templat:Math dst. Hal ini menyebabkan arcsinus bernilai banyak: Templat:Math, tapi juga Templat:Math, Templat:Math, dst. Ketika hanya satu nilai yang diperlukan, nilai fungsi dapat dibatasi hanya ke cabang utama-nya saja. Dengan pembatasan ini, untuk setiap nilai x di domain, ekspresi Templat:Math akan menghasilkan satu nilai tunggal, yang disebut nilai utama. Selang nilai (standar) untuk nilai utama berkisar dari Templat:Math sampai Templat:Math, dan selang nilai (standar) untuk arccos berkisar dari 0 sampai Templat:Math.

$\theta =\arcsin \left(\frac{\text{sisi tegak}}{\text{hipotenusa}}\right)=\arccos \left(\frac{\text{sisi alas}}{\text{hipotenusa}}\right).$

dengan (untuk suatu bilangan bulat k):

$\begin{array}{cc}\sin (y)=x⟺& y=\arcsin (x)+2\pi k,\text{ atau }\\ & y=\pi -\arcsin (x)+2\pi k\\ \cos (y)=x⟺& y=\arccos (x)+2\pi k,\text{ atau }\\ & y=-\arccos (x)+2\pi k\end{array}$

Berdasarkan definisi, arcsin dan arccos memenuhi persamaan-persamaan berikut:

$\sin (\arcsin (x))=x\cos (\arccos (x))=x$

dan

$\begin{array}{cc}\arcsin (\sin (\theta ))=\theta & \text{untuk}-\frac{\pi }{2}\le \theta \le \frac{\pi }{2}\\ \arccos (\cos (\theta ))=\theta & \text{untuk}0\le \theta \le \pi \end{array}$

Kalkulus

Turunan dari sinus dan kosinus adalah:

$\frac{d}{dx}\sin (x)=\cos (x)\frac{d}{dx}\cos (x)=-\sin (x)$

Sedangkan antiturunan mereka adalah:

$\int \sin (x)dx=-\cos (x)+C$

$\int \cos (x)dx=\sin (x)+C$

dengan C menyatakan konstanta integrasi.

Sinus dan kosinus muncul sebagai solusi untuk persamaan diferensial $$f^{″}(x)=-kf(x)$$

Persamaan tersebut muncul pada banyak sistem fisik, seperti pada pendulum maupun pada beban yang terikat pada suatu pegas. Solusi persamaan ini adalah: $$f(x)=C_1\sin (x\sqrt{k})+C_2\cos (x\sqrt{k})$$

Ketika k = 1, solusi unik dengan f(0) = 0 dan f'(0) = 1 adalah fungsi sinus, dan solusi unik dengan f(0) = 1 dan f'(0) = 0 adalah fungsi kosinus.

Identitas trigonometri Pythagoras

Hubungan dasar antara fungsi sinus dan kosinus termuat dalam identitas trigonometri Pythagoras:

${\cos }^2(\theta )+{\sin }^2(\theta )=1$

dengan sin²(x) menyatakan (sin(x))².

Rumus sudut ganda

Fungsi sinus diwarnai biru dan fungsi kuadrat sinus (sin²(x)) diwarnai merah. Sumbu-x dinyatakan dalam satuan radian.

Sinus dan kosinus memenuhi persamaan-persamaan sudut ganda berikut:

$\sin (2\theta )=2\sin (\theta )\cos (\theta )$

$\cos (2\theta )={\cos }^2(\theta )-{\sin }^2(\theta )=2{\cos }^2(\theta )-1=1-2{\sin }^2(\theta )$

Rumus sudut ganda kosinus menyimpulkan bahwa fungsi sin² dan cos² adalah gelombang sinus yang mengalami penggeseran dan skalarisasi. Secara spesifik,

${\sin }^2(\theta )=\frac{1-\cos (2\theta )}{2}{\cos }^2(\theta )=\frac{1+\cos (2\theta )}{2}$

Gambar berikut menyajikan fungsi sinus dan fungsi kuadrat sinus, masing-masing diwarnai dengan warna biru dan warna merah. Kedua grafik fungsi memiliki bentuk yang sama, namun memiliki jangkauan fungsi dan periode yang berbeda. Fungsi kuadrat sinus bernilai non-negatif, namun memiliki periode dua kali lebih cepat.

Sifat yang berhubungan dengan kuadran

Keempat kuadran pada sistem koordinat Kartesius.

Tabel berikut menyajikan banyak sifat penting dari fungsi sinus (tanda fungsi, kemonotonan, dan kecekungan), disusun berdasarkan kuadran dari nilai argumen (sudut). Untuk argumen di luar tabel, informasi yang bersesuaian dapat diperoleh dengan menggunakan sifat periodik $\sin (\alpha +360^{\circ })=\sin (\alpha )$ dari fungsi sinus.

Kuadran	Sudut		Sinus			Kosinus
	Derajat	Radian	Tanda	Kemonotonan	Kecekungan	Tanda	Kemonotonan	Kecekungan
Kuadran I	$0^{\circ }<x<90^{\circ }$	$0<x<\frac{\pi }{2}$	$+$	naik	konkaf	$+$	turun	konkaf
Kuadran II	$90^{\circ }<x<180^{\circ }$	$\frac{\pi }{2}<x<\pi$	$+$	turun	konkaf	$-$	turun	konveks
Kuadran III	$180^{\circ }<x<270^{\circ }$	$\pi <x<\frac{3\pi }{2}$	$-$	turun	konveks	$-$	naik	konveks
Kuadran IV	$270^{\circ }<x<360^{\circ }$	$\frac{3\pi }{2}<x<2\pi$	$-$	naik	konveks	$+$	naik	konkaf

Kuadran-kuadran pada lingkaran satuan dan fungsi sin(x), menggunakan sistem koordinat Kartesius.

Tabel berikut menyajikan informasi dasar terkait nilai sinus dan kosinus pada batas selang kuadran.

Derajat	Radian	$\sin (x)$		$\cos (x)$
		Nilai	Jenis titik	Nilai	Jenis titik
$0^{\circ }$	$0$	$0$	Akar, belok	$1$	Maksimum
$90^{\circ }$	$\frac{\pi }{2}$	$1$	Maksimum	$0$	Akar, belok
$180^{\circ }$	$\pi$	$0$	Akar, belok	$-1$	Minimum
$270^{\circ }$	$\frac{3\pi }{2}$	$-1$	Minimum	$0$	Akar, belok

Definisi dengan deret

Fungsi sinus (biru) dapat dihampiri dengan baik dengan polinomial Taylor-nya yang berderajat 7 (merah muda) untuk nilai sudut di antara -Templat:Pi sampai Templat:Pi.

Animasi berikut menunjukkan efek menambahkan lebih banyak suku pada deret Taylor menyebabkannya menjadi lebih mirip dengan fungsi sinus.

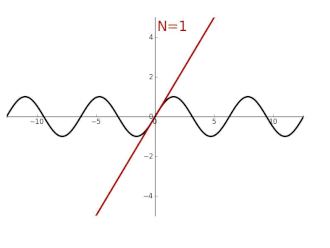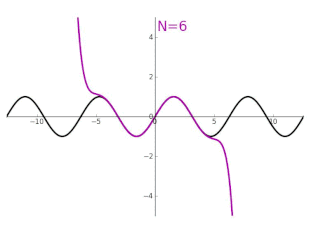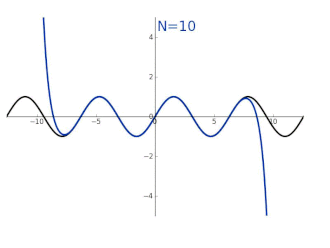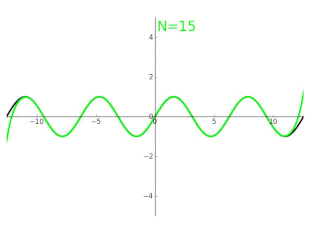
Turunan secara terus-menerus dari fungsi sinus di 0 dapat digunakan untuk menentukan bentuk deret Taylor-nya. Dengan hanya menggunakan geometri dan sifat dari limit, dapat ditunjukkan bahwa turunan dari sinus adalah kosinus, dan turunan kosinus adalah negatif dari sinus. Hal ini mengartikan secara turunan dari sin(x) secara berurutan adalah cos(x), -sin(x), -cos(x), sin(x), dan berulang lagi dari awal. Turunan ke-(4n+k), dievaluasi di titik 0 adalah:

${\sin }^{(4n+k)}(0)=\{\begin{array}{cc}0& \text{ketika }k=0\\ 1& \text{ketika }k=1\\ 0& \text{ketika }k=2\\ -1& \text{ketika }k=3\end{array}$

Dengan simbol pada tika atas (superscript) menyatakan turunan secara berulang. Hal ini dapat digunakan untuk menghitung ekspansi deret Taylor di titik x = 0 (dalam radian):

$\begin{array}{cc}\sin (x)& =x-\frac{x^3}{3!}+\frac{x^5}{5!}-\frac{x^7}{7!}+\cdots \\ & =\sum _{n=0}^{\mathrm{\infty }}\frac{(-1{)}^n}{(2n+1)!}{x}^{2n+1}\\ \end{array}$

Menghitung turunan untuk setiap suku menghasilkan deret Taylor untuk kosinus:

$\begin{array}{cc}\cos (x)& =1-\frac{x^2}{2!}+\frac{x^4}{4!}-\frac{x^6}{6!}+\cdots \\ & =\sum _{n=0}^{\mathrm{\infty }}\frac{(-1{)}^n}{(2n)!}{x}^{2n}\\ \end{array}$

Bentuk pecahan berulang

Fungsi sinus dan kosinus dapat direpresentasikan dalam bentuk pecahan berulang yang diperumum, yang dapat dihasilkan dengan menggunakan rumus pecahan berulang Euler:

$\sin (x)=\frac{x}{1+\frac{x^2}{2\cdot 3-x^2+\frac{2\cdot 3x^2}{4\cdot 5-x^2+\frac{4\cdot 5x^2}{6\cdot 7-x^2+\ddots }}}}.$

$\cos (x)=\frac{1}{1+\frac{x^2}{1\cdot 2-x^2+\frac{1\cdot 2x^2}{3\cdot 4-x^2+\frac{3\cdot 4x^2}{5\cdot 6-x^2+\ddots }}}}.$

Hukum sinus

Templat:Main Hukum sinus menyatakan bahwa untuk sembarang segitiga dengan sisi-sisi a, b, dan c, dan sudut-sudut yang menghadap sisi-sisi tersebut secara berurutan adalah A, B, dan C, berlaku:$$\frac{\sin A}{a}=\frac{\sin B}{b}=\frac{\sin C}{c}.$$Pernyataan di atas ekuivalen dengan persamaan berikut:

$\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}=2R,$

dengan R menyatakan radius dari lingkaran luar segitiga. Hal tersebut dapat ditunjukkan dengan membagi segitiga menjadi dua segitiga siku-siku dan menggunakan definisi sinus.

Hukum sinus berguna untuk menghitung panjang sisi segitiga yang tidak diketahui, jika nilai dua sudut dan satu sisi diketahui. Hal ini umum terjadi ketika melakukan triangulasi, suatu teknik untuk menentukan panjang yang tidak diketahui dengan mengukur dua nilai sudut yang terpisah dalam jarak yang ditentukan sebelumnya.

Hukum kosinus

Templat:Main Hukum kosinus menyatakan bahwa untuk sembarang segitiga dengan sisi-sisi a, b, dan c, dan sudut-sudut yang menghadap sisi-sisi tersebut secara berurutan adalah A, B, dan C, berlaku:$$a^2+b^2-2ab\cos (C)=c^2$$Untuk kasus dengan $C=\pi /2$, nilai $\cos (C)=0$ dan hukum ini berubah menjadi teorema Pythagoras: Untuk segitiga siku-siku, berlaku hubungan $a^2+b^2=c^2,$ dengan c menyatakan panjang hipotenusa.

Nilai-nilai spesial

Beberapa sudut yang umum (θ) tergambarkan pada lingkaran satuan. Sudut-sudut dinyatakan dalam satuan derajat dan radian, beserta titik-titik perpotongan di lingkaran satuan dengan koordinat (cos(θ), sin(θ)).

Untuk beberapa sudut x dalam satuan derajat, nilai dari fungsi sin(x) dan cos(x) dapat dinyatakan dengan sederhana. Berikut adalah tabel beberapa nilai sudut dan fungsi tersebut:

Sudut, x			sin(x)		cos(x)
Derajat	Radians	Putaran	Eksak	Desimal	Eksak	Desimal
0°	0	0	0	0	1	1
15°	Templat:Sfracπ	Templat:Sfrac	$\frac{\sqrt{6}-\sqrt{2}}{4}$	0.2588	$\frac{\sqrt{6}+\sqrt{2}}{4}$	0.9659
30°	Templat:Sfracπ	Templat:Sfrac	Templat:Sfrac	0.5	$\frac{\sqrt{3}}{2}$	0.8660
45°	Templat:Sfracπ	Templat:Sfrac	$\frac{\sqrt{2}}{2}$	0.7071	$\frac{\sqrt{2}}{2}$	0.7071
60°	Templat:Sfracπ	Templat:Sfrac	$\frac{\sqrt{3}}{2}$	0.8660	Templat:Sfrac	0.5
75°	Templat:Sfracπ	Templat:Sfrac	$\frac{\sqrt{6}+\sqrt{2}}{4}$	0.9659	$\frac{\sqrt{6}-\sqrt{2}}{4}$	0.2588
90°	Templat:Sfracπ	Templat:Sfrac	1	1	0	0

Titik tetap

Iterasi titik tetap x_n+1 = cos(x_n) dengan nilai awal x₀ = -1 akan konvergen ke bilangan Dottie.

Nol adalah satu-satunya titik tetap real yang dimiliki fungsi sinus; dengan kata lain, perpotongan antara fungsi sinus dan fungsi identitas $f(x)=x$ hanya terjadi di titik $x=0$. Satu-satunya titik tetap (real) dari fungsi kosinus adalah bilangan Dottie. Dengan kata lain, bilangan Dottie adalah akar real unik dari persamaan $\cos (x)=x.$ Ekspansi desimal dari bilangan Dottie adalah $0.739085...$.

Panjang busur

Panjang busur dari kurva sinus diantara $a$ dan $b$ adalah ${\int }_a^b\sqrt{1+{\cos }^2(x)}dx=\sqrt{2}(\mathrm{E}(b,1/\sqrt{2})-\mathrm{E}(a,1/\sqrt{2}))$, dengan $\mathrm{E}(\phi ,k)$ menyatakan integral eliptik tak lengkap jenis kedua (incomplete elliptic integral of the second kind) dengan modulus $k$.

Panjang busur untuk satu periode penuh adalah $L=4\sqrt{2{\pi }^3}/\mathrm{\Gamma }(1/4{)}^2+\mathrm{\Gamma }(1/4{)}^2/\sqrt{2\pi }=7.640395578\dots$ dengan $\mathrm{\Gamma }$ menyatakan fungsi gamma. Solusi persamaan ini dapat dihitung dengan cepat menggunakan rataan arimetik-geometrik: $L=2\mathrm{M}(1,\sqrt{2})+2\pi /\mathrm{M}(1,\sqrt{2})$. Lebih lanjut, $L$ sebenarnya adalah keliling dari elips dengan panjang sumbu semi-major sebesar $\sqrt{2}$ dan panjang sumbu semi-minor sebesar $1$.

Panjang busur dari kurva sinus dari $0$ sampai $x$ adalah $Lx/(2\pi )$, ditambah suatu faktor koreksi yang bernilai periodik dalam $x$ dan memiliki periode $\pi$. Deret Fourier dari faktor koreksi ini dapat dituliskan dalam bentuk tertutup dengan menggunakan sutu fungsi spesial. Panjang busur kurva sinus dari $0$ sampai $x$ adalah$$(\frac{\mathrm{M}(1,\sqrt{2})}{\pi }+\frac{1}{\mathrm{M}(1,\sqrt{2})})x+\sqrt{2}\sum _{n=1}^{\mathrm{\infty }}\frac{(-1{)}^n(\genfrac{}{}{0ex}{}{n-3/2}{n})}{2^{3n}n}{}_2{F}_1(n-\frac{1}{2},n+\frac{1}{2};2n+1;\frac{1}{2})\sin (2nx),$$dengan ${}_2{F}_1$ menyatakan fungsi hipergeometrik. Suku-suku pada ekspresi di atas dapat diaproksimasi dengan$$1.21600672x+0.10317093\sin (2x)-0.00220445\sin (4x)+0.00012584\sin (6x)-0.00001011\sin (8x)+\cdots$$

Hubungan dengan bilangan kompleks

$\cos (\theta )$ dan $\sin (\theta )$ secara berurutan adalah nilai dari bagian real dan bagian imajiner dari $e^{i\theta }$.

Sinus dan kosinus digunakan untuk menggabungkan bagian real dan bagian imajiner dari suatu bilangan kompleks dengan bentuk koordinat polar (r, φ):$$z=r(\cos (\phi )+i\sin (\phi ))$$Bagian real dan bagian imajiner dari bilangan kompleks tersebut adalah:$$\mathrm{Re}(z)=r\cos (\phi )$$dengan r dan φ menyatakan magnitudo dan sudut dari bilangan kompleks z.

Untuk sembarang bilangan real θ, rumus Euler menyatakan bahwa:$$e^{i\theta }=\cos (\theta )+i\sin (\theta )$$Dengan demikian, jika koordinat polar dari z adalah (r, φ), maka $z=r{e}^{i\phi }.$

Argumen kompleks

Pewarnaan domain dari fungsi sin(z) pada bidang kompleks. Tingkat kecerahan menyatakan magnitudo, sedangkan hue menyatakan argumen kompleks.

sin(z) sebagai suatu medan vektor.

Dengan menerapkan definisi deret dari fungsi sinus dan kosinus ke suatu argumen kompleks z, didapatkan hubungan:

$\begin{array}{cc}\sin (z)& =\sum _{n=0}^{\mathrm{\infty }}\frac{(-1{)}^n}{(2n+1)!}{z}^{2n+1}\\ & =\frac{e^{iz}-e^{-iz}}{2i}\\ & =\frac{\sinh \left(iz\right)}{i}\\ & =-i\sinh \left(iz\right)\\ \cos (z)& =\sum _{n=0}^{\mathrm{\infty }}\frac{(-1{)}^n}{(2n)!}{z}^{2n}\\ & =\frac{e^{iz}+e^{-iz}}{2}\\ & =\cosh (iz)\\ \end{array}$

dengan sinh dand cosh adalah sinus dan cosinus hiperbolik. Kedua fungsi ini merupakan fungsi entire.

Terkadang fungsi sinus dan kosinus kompleks lebih cocok dinyatakan dalam bentuk bagian real dan bagian imajiner. Pada kasus ini, persamaan-persamaan berikut dapat digunakan:

$\begin{array}{cc}\sin (x+iy)& =\sin (x)\cos (iy)+\cos (x)\sin (iy)\\ & =\sin (x)\cosh (y)+i\cos (x)\sinh (y)\\ \cos (x+iy)& =\cos (x)\cos (iy)-\sin (x)\sin (iy)\\ & =\cos (x)\cosh (y)-i\sin (x)\sinh (y)\\ \end{array}$

Grafik kompleks

Fungsi sinus pada bidang kompleks

komponen real	komponen imajiner	magnitudo

Fungsi arcsinus pada bidang kompleks

komponen real	komponen imajiner	magnitudo

Sejarah

Quadrant from 1840s Ottoman Turkey with axes for looking up the sine and versine of angles

Walaupun ilmu trigonometri dapat dilacak jauh ke masa lalu, penggunaan fungsi trigonometri seperti yang digunakan saat ini dikembangkan pada zaman pertengahan. Fungsi busur ditemukan oleh Hipparchus dari Nicaea (180–125 SM) dan Ptolemy dari Mesir Romawi (90–165 M). Secara spesifik, lihat tabel busur Ptolemy.

Fungsi sinus dan versine (1 − kosinus) dapat dilacak ke fungsi jyā dan koṭi-jyā yang digunakan pada bidang astronomi India (Aryabhatiya, Surya Siddhanta) di masa kemaharajaan Gupta (320-550 M). Fungsi ini selanjutnya mengalami penerjemahan dari bahasa Sanskerta ke bahasa Arab, dilanjutkan dari bahasa Arab ke bahasa Latin.

Keenam fungsi trigonometrik yang digunakan saat ini sudah dikenal di masa matematika Islam pada abas ke-9, termasuk hukum sinus yang digunakan untuk menyelesaikan permasalahan yang berkaitan dengan segitiga. Dengan pengecualian sinus, kelima fungsi trigonometrik lain ditemukan oleh matematikawan Arab; yakni fungsi kosinus, tangen, kotangen, sekan, dan kosekan. Al-Khwārizmī (sekitar 780–850) membentuk tabel nilai sinus, kosinus, dan tangen. Muhammad ibn Jābir al-Harrānī al-Battānī (853–929) menemukan fungsi invers dari sekan dan kosekan, dan membentuk tabel kosekan pertama kalinya untuk setiap sudut dari 1° sampai 90°.

Publikasi pertama yang menggunakan singkatan 'sin', 'cos', dan 'tan' adalah oleh matematikawan Prancis Albert Girard; singkatan ini selanjutnya disebarluaskan oleh Euler (lihat bagian dibawah). Tulisan Opus palatinum de triangulis oleh Georg Joachim Rheticus, seorang siswa Copernicus, mungkin adalah yang pertama di Eropa, yang mendefinisikan fungsi-fungsi trigonometri langsung dari segitiga siku-siku ketimbang menggunakan lingkaran. Tulisan ini juga mengikutkan tabel nilai untuk keenam fungsi trigonometrik; tulisan ini diselesaikan oleh seorang siswanya, Valentin Otho, pada tahun 1596.

Dalam suatu makalah yang diterbitkan pada tahun 1682, Leibniz membuktikan bahwa sin x bukanlah suatu fungsi aljabar dari x. Roger Cotes menghitung turunan dari sinus dalam karyanya Harmonia Mensurarum (1722). Karya Introductio in analysin infinitorum (1748) oleh Leonhard Euler adalah yang paling signifikan di Eropa, dalam memberikan dasar analitik mengenai fungsi-fungsi trigonometrik. Dalam karya ini, fungsi-fungsi dinyatakan sebagai deret tak hingga, menyajikan "rumus Euler", dan penggunaan singkatan sin., cos., tang., cot., sec., dan cosec yang mirip dengan penggunaan saat ini.

Etimologi

Secara etimologi, kata sinus berasal dari kata Sanskerta untuk busur, jiva* (jya adalah sinonim yang lebih populer). Kata ini mengalami transliterasi ke bahasa Arab sebagai jiba جيب, yang sebenarnya tidak memiliki arti dari bahasa Arab, dan disingkat sebagai jb جب . Karena bahasa Arab ditulis tanpa menggunakan vokal pendek, "jb" secara keliru diintepretasikan sebagai kata jaib جيب, yang berarti "dada". Ketika teks Arab diterjemahkan ke bahasa Latin oleh Gerard of Cremona pada abad ke-12, ia menggunakan kata yang setara untuk "dada", sinus (yang berarti "dada" atau "teluk" atau "lipatan"). Gerard mungkin bukan yang pertama kali menggunakan terjemahan ini; Robert dari Chester sepertinya terlebih dahulu melakukannya dan terdapat bukti penggunaan pada masa yang lebih lawas. Bentuk bahasa Inggris sine diperkenalkan pada tahun 1590-an. Kata "cosine" berasal dari singkatan bahasa Latin masa pertengahan untuk frasa "complementi sinus".

Implementasi perangkat lunak

Tidak ada standardisasi algoritma untuk menghitung fungsi sinus dan kosinus. IEEE 754-2008, standar paling umum digunakan untuk komputasi titik-kambang (floating-point), tidak membahas cara menghitung fungsi trigonometri seperti sinus. Algoritma yang dikembangkan untuk menghitung sinus dapat disesuaikan dengan menimbang aspek kecepatan, akurasi, portabilitas, maupun jangkauan input yang dapat diproses. Hal ini menyebabkan munculnya banyak algoritma berbeda, khususnya untuk menyelesaikan kasus khusus seperti menghitung input yang sangat besar, seperti sin(10Templat:Sup).

Optimisasi pemrograman yang umum, digunakan khususnya dalam grafik 3D, adalah dengan menghitung tabel nilai sinus terlebih dahulu, misalnya satu nilai untuk setiap derajat, lalu melakukan interpolasi linear dengan menggunakan dua nilai derajat yang paling dekat dengan nilai input. Hal ini memungkinkan hasil ditentukan dari pencarian tabel ketimbang melakukan perhitungan secara real-time. Namun pada arsitektur CPU modern, metode ini mungkin tidak memberikan keuntungan yang berarti.Templat:Citation needed Beberapa arsitektur CPU memiliki instruksi dasar untuk menghitung sinus, contohnya Intel x87 FPUs since the 80387.

Fungsi sinus dan kosinus, beserta fungsi-fungsi trigonometrik lainnya, umum tersedia pada berbagai bahasa pemrograman dan platform. Dalam komputasi, mereka umumnya dikenal sebagai sin dan cos. Pada bahasa pemrograman, sin dan cos umumnya merupakan fungsi dasar (built-in) atau dapat dijumpai di pustaka matematika standar. Sebagai contoh, pustaka standar C mendefinisikan fungsi sinus di dalam pustaka math.h sebagai sin(double), sinf(float), dan sinl(long double). Parameter untuk setiap fungsi ini adalah nilai titik-kambang, dalam satuan radian. Setiap fungsi akan menghasilkan tipe data yang sama dengan inputnya. Banyak fungsi trigonometrik lainnya juga didefinisikan di math.h, seperti kosinus, arcsinus, dan sinus hiperbolik (sinh). Mirip dengan itu, Python mendefinisikan math.sin(x) dan math.cos(x) yang termuat dalam modul math. Fungsi sinus dan kosinus kompleks tersedia dalam modul cmath, contohnya cmath.sin(z) .

Implementasi berdasarkan satuan putaran

Beberapa pustaka perangkat lunak memiliki implementasi sinus dan kosinus menggunakan sudut yang dinyatakan dalam setengah-putaran; nilai dari setengah-putaran adalah sudut sebesar 180 derajat atau $\pi$ radian. Menyatakan sudut dalam satuan putaran atau setengah-putaran memiliki keuntungan akurasi dan efisiensi pada beberapa kasus. Pada MATLAB, OpenCL, R, Julia, CUDA, dan ARM, fungsi-fungsi ini disebut dengan sinpi dan cospi. Sebagai contoh, sinpi(x) akan mengevaluasi nilai to $\sin (\pi x),$ dengan x dinyatakan dalam satuan radian.

Keuntungan akurasi timbul dari kemampuan merepresentasikan sudut-sudut penting, seperti satu putaran penuh, setengah putaran, dan seperempat putaran, dengan sempurna (losslessly) dalam bentuk titik-kambang (floating-point) biner atau titik-tetap (fixed-point). Sebagai kontras, menyatakan $2\pi$, $\pi$, dan $\frac{\pi }{2}$ dalam bentuk titik-kambang biner akan selalu menyebabkan hilangnya akurasi akibat galat pemotongan. Satuan putaran juga memiliki keuntungan akurasi dan efisiensi ketika menghitung modulo satu periode. Komputasi modulo 1 putaran atau modulo 2 setengah-putaran dapat dinyatakan dengan sempurna dan dihitung dengan efisien, baik dalam bentuk titik-kambang maupun titik-tetap. Sebagai contoh, komputasi modulo 1 atau modulo 2 untuk nilai biner dalam bentuk titik-tetap hanya memerlukan operasi penggeseran bit (bit shift) dan operator bit-demi-bit (bitwise) AND. Sebagai kontras, komputasi modulo $\frac{\pi }{2}$ menghasilkan galat karena ketidakakuratan dalam merepresentasikan $\frac{\pi }{2}$.

Untuk aplikasi yang melibatkan sensor sudut, sensor umumnya menyajikan hasil pengukuran yang kompatibel dengan satuan putaran atau setengah-putaran. Sebagai contoh, suatu sensor sudut mungkin memberikan nilai 0 sampai 4096 ketika melakukan satu putaran penuh. Jika setengah-putaran digunakan sebagai satuan pengukuran sudut, maka nilai yang diberikan sensor dapat dipetakan dengan sempurna (lossless) ke tipe data titik-tetap dengan 11 bit dibelakang koma. Sebagai kontras, jika radian yang digunakan untuk menghitung sudut, ketidakakuratan sebesar $\frac{\pi }{2048}$ terjadi ketika nilai dari sensor diubah menjadi satuan radian.

Bacaan lebih lanjut

• Templat:Cite book
• Templat:Citation
• Templat:Citation