Aturan sinus

Untuk kegunaan lain, lihat Sinus (disambiguasi).

Templat:Multiple imageDalam trigonometri, aturan sinus, rumus sinus, atau hukum sinus adalah sebuah persamaan yang memperbandingan panjang sisi-sisi segitiga terhadap sinus sudut-sudutnya. Aturan ini menyatakan bahwa$$\frac{a}{\sin \alpha }=\frac{b}{\sin \beta }=\frac{c}{\sin \gamma }=2R,$$dengan Templat:Math, dan Templat:Math menyatakan panjang-panjang sisi dari segitiga, dan Templat:Math, dan Templat:Math adalah besar sudut-sudut yang menghadap sisi-sisi tersebut (lihat gambar sebagai ilustrasi), sedangkan Templat:Math adalah radius dari lingkaran luar segitiga. Jika radius lingkaran tidak digunakan, aturan sinus terkadang dinyatakan dalam bentuk$$\frac{\sin \alpha }{a}=\frac{\sin \beta }{b}=\frac{\sin \gamma }{c}.$$Aturan sinus berguna untuk menghitung sisi yang belum diketahui dari suatu segitiga apabila besar dua sudut dan panjang satu sisinya diketahui. Ini adalah masalah yang umum terjadi ketika melakukan triangulasi. Rumus ini juga dapat digunakan bila diketahui panjang dua sisi dan besar sudut yang tak diapit kedua sisi tersebut. Dalam kasus ini, data mungkin tidak dapat menghasilkan segitiga yang unik, sehingga rumus dapat memberikan dua nilai yang mungkin untuk sudut yang diapit. Aturan sinus juga dapat dipakai untuk menghitung jari-jari lingkaran luar segitiga.

Aturan sinus adalah salah satu dari dua persamaan trigonometrik yang umum digunakan untuk menentukan besar panjang dan sudut pada segitiga, persamaan lain yang digunakan adalah aturan kosinus.

Aturan sinus dapat diperumum ke dimensi yang lebih tinggi, yakni pada permukaan dengan kurvatur yang bernilai konstan.

Sejarah

Hukum sinus bagi segitiga yang terletak pada bola ditemukan pada abad ke-10. Penemuan ini banyak diatribusikan kepada Abu-Mahmud Khojandi, Abul Wafa Muhammad Al Buzjani, Nashiruddin ath-Thusi, dan Abu Nashr Mansur.

Pada abad ke-11, buku Ibn Muʿādh al-Jayyānī' mengandung hukum sinus secara umum. Hukum sinus pada bidang [datar] kemudian dinyatakan oleh Nashiruddin ath-Thusi pada abad ke-13. Dalam karyanya Tentang Gambar Sektor, ia menuliskan hukum sinus untuk bidang datar dan untuk permukaan bola, dan memberikan rumus untuk kedua hukum ini.

Pada abad ke-15, matematikawan Jerman Regiomontanus menggunakan hukum sinus sebagai fondasi solusi tentang masalah yang berkaitan dengan segitiga siku-siku. Solusi yang tertulis pada Buku IV-nya pada gilirannya menjadi dasar solusi masalah yang berkaitan dengan segitiga secara umum.

Bukti

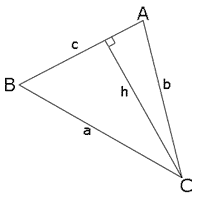
Perhatikan segitiga dengan sisi a, b, dan c, dan sudut yang berhadapan A, B, dan C. Tarik garis tinggi h dari sudut C ke sisi c sehingga segitiga ABC terbagi menjadi dua segitiga siku-siku.

Dapat diamati bahwa:

$\sin A=\frac{h}{b}$ dan$\sin B=\frac{h}{a}$

Dari persamaan tersebut, dapat diturunkan dua bentuk dari h

$h=b\sin A=a\sin B$

sehingga diperoleh

$\frac{\sin A}{a}=\frac{\sin B}{b}.$

Memperlakukan garis tinggi dari sudut A dengan cara yang sama, kemudian akan diperoleh:

$\frac{\sin B}{b}=\frac{\sin C}{c}$

Kasus ambigu

Ketika menggunakan aturan sinus untuk menentukan panjang sisi suatu segitiga, kasus ambigu dapat terjadi ketika terdapat dua segitiga dapat dibuat dari informasi yang diketahui (dengan kata lain, akan menghasilkan dua solusi berbeda). Kasus ini mungkin saja terjadi karena ada dua nilai sudut yang benar antara 0° dan 180° yang memiliki nilai sinus yang sama.

Kasus ambigu penggunaan aturan sinus untuk mencari panjang sisi segitiga. Apabila diberikan besar sudut $\alpha$, juga panjang sisi $a$ dan $c$, maka kedua-dua segitiga Templat:Math dan Templat:Math adalah benar.

Untuk sembarang segitiga, kasus ambigu terjadi apabila kondisi-kondisi berikut terpenuhi:

• Informasi yang tersedia tentang segitiga hanyalah sudut Templat:Math dan panjang Templat:Math dan Templat:Math.
• Sudut Templat:Math lancip (yakni, besar sudut Templat:Math < 90°).
• Sisi Templat:Math lebih pendek daripada sisi Templat:Math (yakni, besar Templat:Math).
• Sisi Templat:Math lebih panjang daripada ketinggian Templat:Math ketika diukur dari titik Templat:Math (artinya Templat:Math), dengan nilai Templat:Math.

Jika semua kondisi tersebut terpenuhi, maka sudut Templat:Math dan Templat:Math menghasilkan dua segitiga yang valid tapi berbeda, mengartikan dua persamaan berikut benar:$$\gamma \text{'}=\arcsin \frac{c\sin \alpha }{a}\text{atau}\gamma =\pi -\arcsin \frac{c\sin \alpha }{a}.$$Dari persamaan di atas, dapat ditentukan besar sudut Templat:Math dan panjang sisi Templat:Math, atau besar sudut Templat:Math dan panjang sisi Templat:Math, jika diperlukan.

Contoh

Contoh 1

Diberikan informasi: panjang sisi Templat:Math, sisi Templat:Math, dan sudut Templat:Math, sedangkan nilai sudut Templat:Math ingin dicari. Menggunakan aturan sinus, disimpulkan bahwa$$\frac{\sin \alpha }{20}=\frac{\sin (40^{\circ })}{24}.$$ Sehingga dengan menggunakan invers dari fungsi sinus, arcsinus, didapatkan $$\alpha =\arcsin \left(\frac{20\sin (40^{\circ })}{24}\right)\approx 32.39^{\circ }.$$Solusi lain dari arcsin adalah nilai Templat:Math. Namun ini tidak digunakan karena akan menghasilkan solusi dengan total sudut segitiga Templat:Math.

Hubungan dengan lingkaran luar segitiga

Pada identitas$$\frac{a}{\sin \alpha }=\frac{b}{\sin \beta }=\frac{c}{\sin \gamma },$$ketiga pecahan tersebut memiliki nilai yang sama dengan panjang diameter dari lingkaran luar segitiga. Bukti mengenai hal ini dapat ditelusuri sampai ke Ptolemy.

Bukti

Membuktikan nilai rasio pada aturan sinus sama dengan panjang diameter lingkaran luar segitiga. Perhatikan bahwa segitiga Templat:Math melalui pusat lingkaran yang berdiameter Templat:Math.

Seperti terlihat pada gambar, misalkan ada sebuah lingkaran yang memuat segitiga $\mathrm{△}ABC$, dan memuat segitiga lain $\mathrm{△}ADB$ yang sisinya melewati pusat lingkaran O. Sudut $\mathrm{\angle }AOD$ memiliki sudut pusat sebesar $180^{\circ }$, sehingga sudut $\mathrm{\angle }ABD=90^{\circ }$. Karena merupakan segitiga siku-siku, pada segitiga $\mathrm{△}ABD$ berlaku$$\sin \delta =\frac{\text{depan}}{\text{miring}}=\frac{c}{2R},$$

dengan $R=\frac{d}{2}$ adalah jari-jari dari lingkaran yang memuat segitiga. Sudut $\gamma$ dan $\delta$ memiliki sudut pusat yang sama, sehingga besar sudut mereka sama: $\gamma =\delta$. Maka disimpulkan,$$\sin \delta =\sin \gamma =\frac{c}{2R}.$$Dengan menyusun kembali suku-suku, dihasilkan$$2R=\frac{c}{\sin \gamma }.$$Proses di atas dapat diulangi dengan membentuk $\mathrm{△}ADB$ yang berbeda, sehingga menghasilkan persamaan

$\frac{a}{\sin \alpha }=\frac{b}{\sin \beta }=\frac{c}{\sin \gamma }=2R.$

Hubungan dengan luas segitiga

Menggunakan notasi yang sama dengan bagian sebelumnya, luas dari segitiga $\mathrm{△}ABC$ adalah $L=\frac{1}{2}ab\sin \gamma$, dengan $\gamma$ adalah sudut yang diapit oleh sisi Templat:Math dan Templat:Math. Mensubtitusi aturan sinus pada persamaan luas segitiga menghasilkan $$L=\frac{1}{2}ab\cdot \frac{c}{2R}=\frac{abc}{4R}.$$Dapat ditunjukkan bahwa persamaan tersebut mengimplikasikan$$\begin{array}{cc}\frac{abc}{2L}& =\frac{abc}{2\sqrt{s(s-a)(s-b)(s-c)}}\\ & =\frac{2abc}{\sqrt{{(a^2+b^2+c^2)}^2-2(a^4+b^4+c^4)}},\end{array}$$dengan $s$ adalah panjang setengah keliling segitiga, yakni $s=\frac{a+b+c}{2}.$ Persamaan ini dapat disederhanakan menjadi rumus Heron untuk menghitung luas segitiga.

Aturan sinus juga dapat digunakan untuk menghasilkan rumus berikut untuk menghitung luas lingkaran. Dengan menyatakan $S=\frac{\sin A+\sin B+\sin C}{2}$, dapat ditunjukkan

$T=4R^2\sqrt{S(S-\sin A)(S-\sin B)(S-\sin C)}$

Kasus hiperbolik

Templat:See also Dalam geometri hiperbolik dengan kurvatur bernilai −1, aturan sinus berubah menjadi$$\frac{\sin A}{\sinh a}=\frac{\sin B}{\sinh b}=\frac{\sin C}{\sinh c}.$$Pada kasus khusus dengan Templat:Math berupa sudut siku-siku, dihasilkan$$\sin C=\frac{\sinh c}{\sinh b}$$yang mirip dengan rumus pada geometri Euklides, yang menyatakan sinus sebagai perbandingan panjang sisi berlawanan dengan sisi hipotenusa.

Pada permukaan bola

Ilustrasi dari setiap label untuk aturan sinus pada permukaan bola.

Aturan sinus pada permukaan bola memberikan hubungan trigonometrik pada segitiga yang sisi-sisinya berupa lingkaran besar.

Misalkan radius dari bola adalah 1. Misalkan pula Templat:Math, Templat:Math, dan Templat:Math adalah panjang dari segmen-segmen lingkaran besar yang menjadi sisi-sisi segitiga. Karena bola berupa bola satuan, panjang Templat:Math, Templat:Math, dan Templat:Math sama dengan besar-besar sudut (dalam radian) dari pusat bola, yang membentuk segmen-segmen lingkaran besar. Misalkan juga Templat:Math, Templat:Math, dan Templat:Math adalah sudut-sudut yang berhadapan dengan masing-masing sisi segitiga. Aturan sinus pada permukaan bola menyatakan bahwa$$\frac{\sin A}{\sin a}=\frac{\sin B}{\sin b}=\frac{\sin C}{\sin c}.$$

Pada permukaan dengan kurvatur konstan

Pada permukaan secara umum, fungsi sinus dapat diperumum sebagai berikut:$${\sin }_{K}x=x-\frac{K{x}^3}{3!}+\frac{K^2{x}^5}{5!}-\frac{K^3{x}^7}{7!}+\cdots .$$yang nilainya juga bergantung kurvatur Templat:Math di posisi $x$ berada. Aturan sinus pada permukaan kurvatur bernilai konstan Templat:Math menyatakan bahwa$$\frac{\sin A}{{\sin }_{K}a}=\frac{\sin B}{{\sin }_{K}b}=\frac{\sin C}{{\sin }_{K}c}.$$Mensubtitusi nilai Templat:Math, Templat:Math, dan Templat:Math, secara berurutan akan menghasilkan aturan sinus pada permukaan Euklides, bola, dan hiperbolik, yang dijelaskan pada bagian-bagian sebelumnya. Misalkan Templat:Math menyatakan keliling lingkaran berdiameter Templat:Math pada ruang dengan kurvatur konstan Templat:Math. Maka Templat:Math. Akibatnya, aturan sinus juga dapat ditulis ulang sebagai:$$\frac{\sin A}{p_K(a)}=\frac{\sin B}{p_K(b)}=\frac{\sin C}{p_K(c)}.$$Rumus ini ditemukan oleh János Bolyai.

Lihat pula

• Triangulasi
• Aturan kosinus