Daftar identitas logaritma

Templat:InfoboxIdentitas logaritma atau dikenal sebagai hukum logaritma, ialah kumpulan rumus-rumus yang melibatkan logaritma dan bertujuan untuk mempermudah kalkulasi pada bentuk-bentuk yang cukup rumit.

Fungsi logaritma dapat didefinisikan sebagai

$b^x=c⟺{}^b\log c=x$.

dimana $b$ adalah adalah basis atau bilangan pokok dari logaritma, dengan syarat $0<b<1$ atau $b>1$, $x$ adalah bilangan yang dilogaritmakan yang disebut dengan numerus, dan bilangan positif $c$ adalah hasil dari logaritma yang disebut dengan antilogaritma.Templat:Butuh rujukan

Sebagai catatan, notasi logaritma yang dipakai dalam halaman ini tetap memiliki makna yang sama dengan ${\log }_{b}x$, kendatipun notasinya berbeda.

Berikut adalah daftar identitas logaritma beserta dengan pembuktian-pembuktiannya, antara lain:

Sifat dasar

Sifat trivial

Salah satu yang paling mendasar dalam identitas logaritma, ialah $b^{}\log b=1$, karena $b^1=b$. Terdapat sifat dasar lain, yaitu

• $b^{}\log 1=0$, karena $b^0=1$.
• $b^{}\log b^n=n$.

Sebagai pengecualian, logaritma dengan $b=0$ tidak memiliki nilai. Hasil limit dari $b^{}\log 0=-\mathrm{\infty }$ ketika $b\to 0^{+}$. Untuk memahami lebih lanjut mengenai konsep ini, lihat buktinya di sini.

Perkalian dan pembagian

• $b^{}\log xy={}^b\log x+{}^b\log y$

Templat:Collapse top Misalkan $b^{}\log x=u$ dan $b^{}\log y=v$. Dengan mengubah ke dalam bentuk eksponen diperoleh $x=b^u$ dan $y=b^v$. Maka,

$xy=b^{u+v}$.

Ambil logaritma basis $a$ pada kedua ruas sehingga

$b^{}\log xy={}^b\log b^{u+v}=u+v={}^b\log x+{}^b\log y◼$.Templat:Butuh rujukan

Templat:Collapse bottomSifat ini dapat diperumum ke kasus dengan numerus merupakan hasil perkalian banyak suku,

$b^{}\log \left(\prod _{i=1}^n{x}_i\right)=\sum _{i=1}^n{}^b\log x_i$.

• $b^{}\log \left(\frac{x}{y}\right)={}^b\log x-{}^b\log y$

Templat:Collapse top Misalkan $b^{}\log x=u$ dan $b^{}\log y=v$. Dengan mengubah ke dalam bentuk eksponen diperoleh $x=b^u$ dan $y=b^v$. Maka, $\frac{x}{y}=b^{u-v}$

Ambil logaritma basis $a$ pada kedua ruas sehingga

$b^{}\log \frac{x}{y}={}^b\log b^{u-v}=u-v={}^b\log x-{}^b\log y◼$.Templat:Butuh rujukan

Penambahan dan pengurangan

• $b^{}\log (x+y)={}^b\log (x)+{}^b\log (1+\frac{y}{x})$
• $b^{}\log (x-y)={}^b\log x+{}^b\log (1-\frac{y}{x})$

Lebih umumnya lagi,

$b^{}\log \left(\sum _{i=0}^n{x}_i\right)={}^b\log x_0+{}^b\log (1+\sum _{i=1}^n\frac{a_i}{a_0})={}^b\log x_0+{}^b\log (1+\sum _{i=1}^n{b}^{({}^b\log x_i{-}^b\log x_0)})$.

Perubahan basis

Perubahan basis dapat dirumuskan sebagai

$b^{}\log x=\frac{{}^p\log x}{{}^p\log b}$

dengan syarat $0<p<1$ dan $p>1$ dan $p\ne 1$, dengan mengikuti definisi logaritma.Templat:Collapse topMisal $b^{}\log x=y$. Dengan mengubah ke dalam bentuk eksponen, kita memperoleh $b^y=x$. Maka, kita tuliskan sebagai

$p^{}\log x{=}^p\log b^y$

Dengan menggunakan sifat sebelumnya, maka

$\begin{array}{cc}{}^p\log x& =y{}^p\log b\\ y& =\frac{{}^p\log x}{{}^p\log b}\end{array}$

Substitusi kembali sehingga didapati

$b^{}\log x=\frac{{}^p\log x}{{}^p\log b}◼$.

Perkalian dan pembagian dalam basis logaritma

• ${bc}^{}\log x=\frac{1}{\frac{1}{{}^b\log x}+\frac{1}{{}^c\log x}}$
• ${\frac{b}{c}}^{}\log x=\frac{1}{\frac{1}{{}^b\log x}-\frac{1}{{}^c\log x}}$

Pertukaran basis

Pertukaran basis pada logaritma dapat dirumuskan sebagai

$b^{}\log x=\frac{1}{{}^x\log b}$.

Templat:Collapse top Dengan menggunakan sifat perubahan basis, maka kita dapat memisalkan $p=x$ akan memperoleh

$b^{}\log x=\frac{{}^x\log x}{{}^x\log b}=\frac{1}{{}^x\log b}$. $◼$Templat:Butuh rujukan

Logaritma dalam eksponen

• $x^{\frac{\log (\log x)}{\log x}}=\log x$ atau $x^{\frac{\log a}{\log x}}=a$

Templat:Collapse top Menggunakan sifat perubahan basis, akan memperoleh

$x^{\frac{\log a}{\log x}}=x^{{}^x\log a}=a$. $◼$

Membatalkan eksponen

Sama halnya dengan penambahan dan pengurangan, maupun perkalian dan pembagian, logaritma dapat membatalkan eksponen karena kedua operasi tersebut saling invers. Secara matematis ini mengartikan,

$b^{{}^b\log x}=x$ karena $b^{}\mathrm{antilog}({}^b\log x)=x$; dan

$b^{}\log (b^x)=x$ karena $b^{}\log ({}^b\mathrm{antilog}x)=x$.

Perhatikan bahwa sifat logaritma di atas dapat kita pakai untuk membuktikan bahwa $b^{}\log x^{\frac{1}{n}}=\frac{1}{n}{}^b\log x$.

Logaritma dengan basis lain

Logaritma natural

• $\ln 1=0$
• $\ln e=1$
• $\ln e^x=x$
• $e^{\ln x}=x$
• $\ln xy=\ln x+\ln y$
• $\ln \frac{x}{y}=\ln x-\ln y$

Logaritma dalam kalkulus

Limit

Untuk $b>1$, ketika $x\to 0^{+}$, maka grafik menunjukkan bahwa nilai yang diperoleh menuju $-\mathrm{\infty }$ dengan drastis dan ketika $x\to \mathrm{\infty }$, maka menuju $\mathrm{\infty }$ secara perlahan.

• $\underset{x\to 0^{+}}{\lim }{}^b\log x=-\mathrm{\infty }$
• $\underset{x\to \mathrm{\infty }}{\lim }{}^b\log x=\mathrm{\infty }$

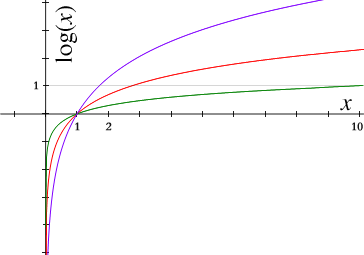
Untuk membuktikan limit tersebut, perhatikan grafik fungsi logaritma basis $b$ sembarang (untuk $b>1$). Sebagai catatan, untuk $0<b<1$,

• $\underset{x\to 0^{+}}{\lim }{}^b\log x=\mathrm{\infty }$
• $\underset{x\to \mathrm{\infty }}{\lim }{}^b\log x=-\mathrm{\infty }$

Pembuktian yang serupa terhadap limit dari fungsi logaritma alami.

• $\underset{x\to 0^{+}}{\lim }\ln x=-\mathrm{\infty }$
• $\underset{x\to \mathrm{\infty }}{\lim }\ln x=\mathrm{\infty }$

Sebagai tambahan, berikut adalah identitas logaritma dalam limit.

• $\underset{x\to 0^{+}}{\lim }{x}^c\cdot {}^b\log x=0$ jika $c>0$
• $\underset{x\to 0^{+}}{\lim }\frac{{}^b\log x}{x^c}=0$ jika $c>0$

Turunan

Turunan logaritma dalam kalkulus dapat dirumuskan sebagai

$\frac{\mathrm{d}}{\mathrm{d}x}{\log }_b(x)=\frac{1}{x\ln (b)}$, dengan $x>0$, $b>0$, dan $b\ne 1$.

Templat:Collapse topPerhatikan bahwa

$y={\log }_{b}x$ jika dan hanya jika $x=b^y$,

maka kita memperoleh

$\ln x=y\cdot \ln b$.

Dengan substitusi kembali, diperoleh

${\log }_{b}x=\frac{\ln x}{\ln b}$.

Jika kita turunkan, maka kita mendapatkan

$\frac{\mathrm{d}}{\mathrm{d}x}{\log }_b(x)=\frac{1}{x\ln (b)}$

Templat:Collapse bottomTurunan dalam basis lain, antara lain

• $\frac{\mathrm{d}}{\mathrm{d}x}\ln x=\frac{1}{x}$

Integral

Integral logaritma dalam kalkulus dapat dirumuskan sebagai

$\int {\log }_b(x)dx=x{\log }_b(x)-\frac{x}{\ln (b)}+C=x({\log }_b(x)-\frac{1}{\ln (b)})+C$

Integral dalam basis lain, antara lain

• $\int \ln (x)dx=x\ln (x)-x+C$

Templat:Collapse top Buktinya dapat kita pakai identitas integral terhadap logaritma, dengan memisalkan $b=e$. Ada bukti lain, ialah integrasi parsial. Dengan memisalkan $u=\ln x$, $\mathrm{d}v=\mathrm{d}x$, $\mathrm{d}u=\frac{1}{x}\mathrm{d}x$ dan $v=x$, maka

$\int \ln x\mathrm{d}x=(\ln x)(x)-\int (x)\left(\frac{1}{x}\right)\mathrm{d}x=x\ln x-\int \mathrm{d}x=x\ln x-x+C$. $◼$

Templat:Collapse bottomSebagai catatan, halaman ini hanya menjelaskan dasar-dasarnya saja. Lihat Daftar integral dari fungsi logaritmik sebagai identitas tambahannya.

Deret

• $\ln (1+x)=\sum _{n\ge 1}\frac{(-1{)}^{n-1}{x}^n}{n}$

Pendekatan logaritma

• $\log x\approx \frac{x^x-1}{x}$
• $\log (1+x)\approx x$

Bentuk pecahan berlanjut

Logaritma alami

• $\ln (1+x)=\frac{x}{1-0x+\frac{1^{2}x}{2-1x+\frac{2^{2}x}{3-2x+\frac{3^{2}x}{4-3x+\frac{4^{2}x}{5-4x+\ddots }}}}}$

• $\ln (1+\frac{x}{y})=\frac{x}{y+\frac{1x}{2+\frac{1x}{3y+\frac{2x}{2+\frac{2x}{5y+\frac{3x}{2+\ddots }}}}}}=\frac{2x}{2y+x-\frac{(1x{)}^2}{3(2y+x)-\frac{(2x{)}^2}{5(2y+x)-\frac{(3x{)}^2}{7(2y+x)-\ddots }}}}$

Lihat pula

• Daftar identitas eksponensiasi