Sifat Archimedes

Ilustrasi sifat Archimedes.

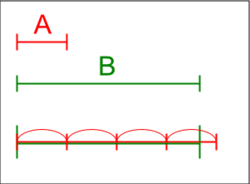
Dalam aljabar abstrak dan analisis, Sifat Archimedes, dinamai menurut ahli matematika Yunani kuno Archimedes dari Sirakusa, adalah sifat yang dimiliki oleh beberapa struktur aljabar, seperti grup, dan medan. Secara kasar, ini adalah sifat yang tidak memiliki elemen jauh lebih besar atau jauh lebih kecil . Adalah Otto Stolz yang memberi nama pada aksioma Archimedes karena muncul sebagai Aksioma V dari Archimedes Pada Bola dan Tabung .

Gagasan tersebut muncul dari teori besaran Yunani Kuno; itu masih memainkan peran penting dalam matematika modern seperti aksioma David Hilbert untuk geometri, dan teori grup terurut, medan terurut, dan medan lokal.

Struktur aljabar di mana dua elemen bukan nol adalah sebanding , dalam arti bahwa tidak satu pun dari mereka sangat kecil dibandingkan dengan yang lain, dikatakan Archimedes. Suatu struktur yang memiliki sepasang elemen bukan nol, yang salah satunya sangat kecil terhadap yang lain, dikatakan sebagai tak-Archimedes. Misalnya, grup terurut linear yang merupakan Archimedes adalah grup Archimedes.

Ini dapat dibuat tepat dalam berbagai konteks dengan rumusan yang sedikit berbeda.Misalnya, dalam konteks kolom terurut, satu memiliki aksioma Archimedes yang merumuskan sifat ini, di mana medan bilangan riil adalah Archimedes, tetapi fungsi rasional dalam koefisien riil tidak.

Sejarah dan asal nama sifat Archimedes

Konsep ini dinamai oleh Otto Stolz (pada tahun 1880-an) setelah ahli geografi dan fisikawan Yunani kuno Archimedes dari Sirakusa.

Sifat Archimedes muncul di Buku V dari Elemen Euklides sebagai Definisi 4:

Karena Archimedes mengkreditkannya ke Eudoksos dari Knidos itu juga dikenal sebagai "Teorema Eudoxus" atau aksioma Eudoxus.

Archimedes menggunakan infinitesimal dalam argumen heuristik, meskipun ia menyangkal bahwa argumen tersebut telah selesai bukti matematika.

Definisi untuk grup terurut linear

MisalkanTemplat:Mvar danTemplat:Mvar menjadi elemen positif dari grup terurut linier G .

KemudianTemplat:Mvar inifintesimal terhadap Templat:Mvar (atau ekuivalen,Templat:Mvar takhingga terhadapTemplat:Mvar) jika, untuk setiap bilangan asli Templat:Mvar, kelipatanTemplat:Math kurang dari Templat:Mvar, yaitu, pertidaksamaan berikut berlaku:

$\underset{n\text{ suku}}{\underbrace{x+\dots +x}}<y$

Definisi ini dapat diperluas ke seluruh kelompok dengan mengambil nilai mutlak.

Grup Templat:Mvar adalah Archimedes jika tidak ada pasangan Templat:Math sedemikian rupa sehingga Templat:Mvar sangat kecil dibandingkan dengan Templat:Mvar.

Selain itu, jika Templat:Mvar adalah struktur aljabar dengan satuan (1) misalnya, gelanggang ,definisi serupa berlaku untuk Templat:Mvar. Jika Templat:Mvar sangat kecil dibandingkan dengan 1, maka Templat:Mvar adalah elemen yang sangat kecil. Demikian juga, jikaTemplat:Mvar tak hingga 1, maka Templat:Mvar adalah elemen takhingga. Struktur aljabar Templat:Mvar adalah Archimedes jika tidak memiliki elemen takhingga dan tidak memiliki elemen takhingga.

Medan terurut

Medan terurut memiliki beberapa sifat tambahan:

• Bilangan rasional adalah terbenam di setiap medan terurut. Artinya, setiap kolom terurut memiliki karakteristik nol.
• JikaTemplat:Mvar Infinitesimal, maka Templat:Math tidak terbatas, dan sebaliknya. Oleh karena itu, untuk memverifikasi bahwa medan adalah Archimedes, cukup dengan memeriksa hanya bahwa tidak ada elemen yang sangat kecil, atau untuk memeriksa bahwa tidak ada elemen yang tak terbatas.
• JikaTemplat:Mvar sangat kecil dan r adalah bilangan rasional, maka Templat:Math juga sangat kecil. Akibatnya, diberi elemen umum Templat:Mvar, tiga bilangan Templat:Math, Templat:Mvar, dan Templat:Math bisa jadi semua sangat kecil atau semua bukan sangat kecil.

Dalam setelan ini, medan terurutTemplat:Mvar adalah Archimedes persis ketika pernyataan berikut, disebut aksioma Archimedes, menyatakan:

"MisalkanTemplat:Mvar adalah elemen apa pun dari Templat:Mvar. Kemudian ada bilangan asli Templat:Mvar sehingga Templat:Math."

Sebagai alternatif, seseorang dapat menggunakan karakterisasi berikut:

$\mathrm{\forall }\epsilon \in K(\epsilon >0⟹\mathrm{\exists }n\in N:1/n<\epsilon ).$

Definisi untuk medan ternorma

Kualifikasi "Archimedes" juga diformulasikan dalam teori peringkat satu medan nilai dan ruang ternorma atas peringkat satu medan nilai sebagai berikut.

Misalkan Templat:Mvar adalah medan yang diberkahi dengan fungsi nilai mutlak, yaitu fungsi yang mengaitkan bilangan real 0 dengan elemen medan 0 dan mengaitkan bilangan riil positif

$|x|$

dengan setiap bukan nol Templat:Math dan dirumuskan

$|xy|=|x||y|$

dan

$|x+y|\le |x|+|y|$

.

Kemudian, Templat:Mvar dikatakan Archimedes jika ada bukan nol Templat:Math ada bilangan asli Templat:Mvar dirumuskan

$|\underset{n\text{ terms}}{\underbrace{x+\cdots +x}}|>1.$

Demikian pula, ruang bernorma adalah Archimedes jika jumlah Templat:Mvar suku, masing-masing sama dengan vektor bukan-nol Templat:Mvar, memiliki norma yang lebih besar dari satu untuk cukup besar Templat:Mvar.

medan dengan nilai mutlak atau ruang bernorma adalah Archimedes atau memenuhi ketentuan yang lebih kuat, yang disebut sebagai ultrametrik pertidaksamaan segitiga$|x+y|\le \max (|x|,|y|)$,

masing-masing. medan atau ruang bernorma yang memenuhi pertidaksamaan segitiga ultrametrik disebut tak-Archimedes.

Konsep ruang linier bernorma tak-Archimedes diperkenalkan oleh A. F. Monna.

Lihat pula

• Templat:Annotated link
• Templat:Annotated link
• Templat:Annotated link

Referensi

• Templat:Cite book